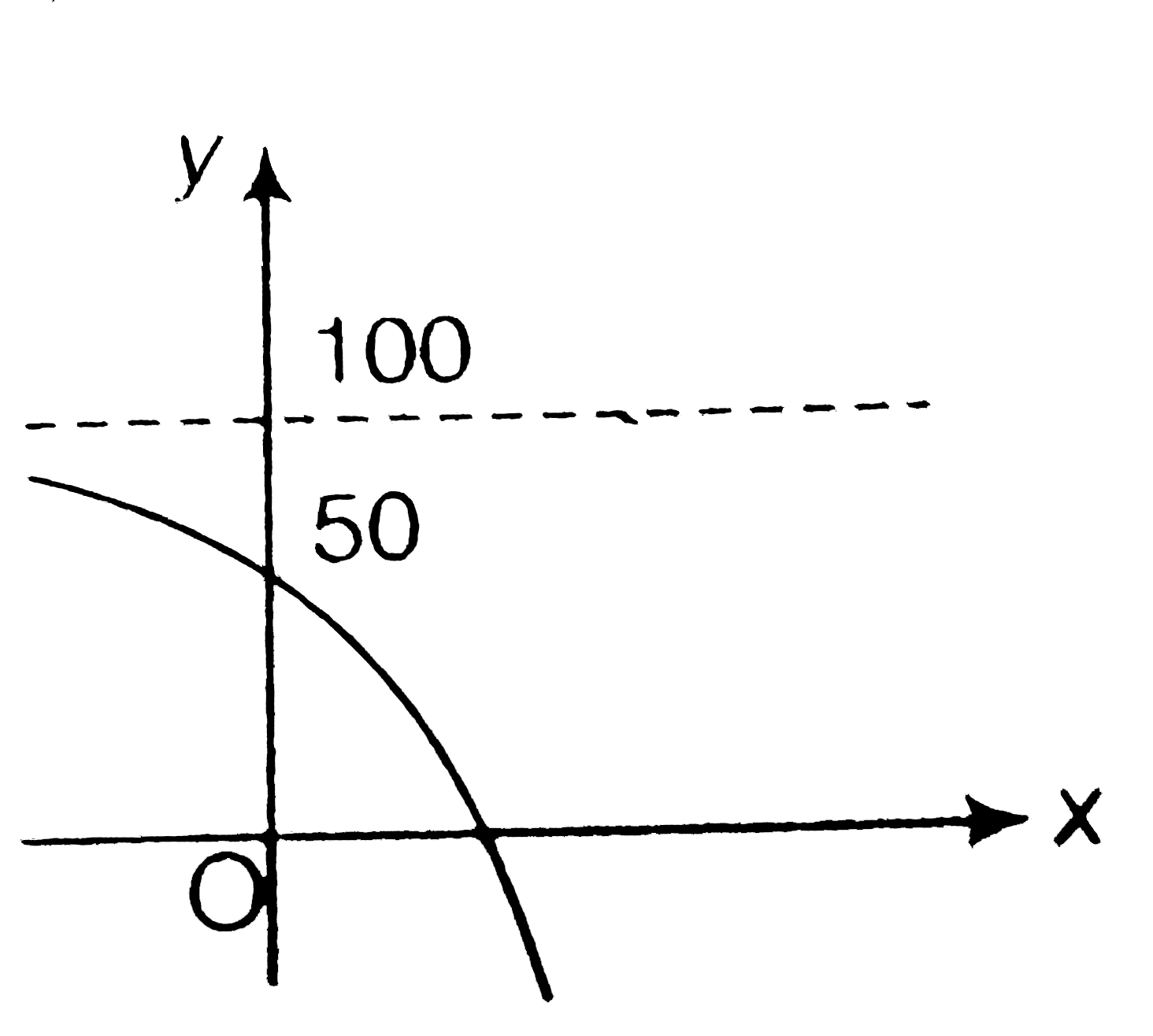
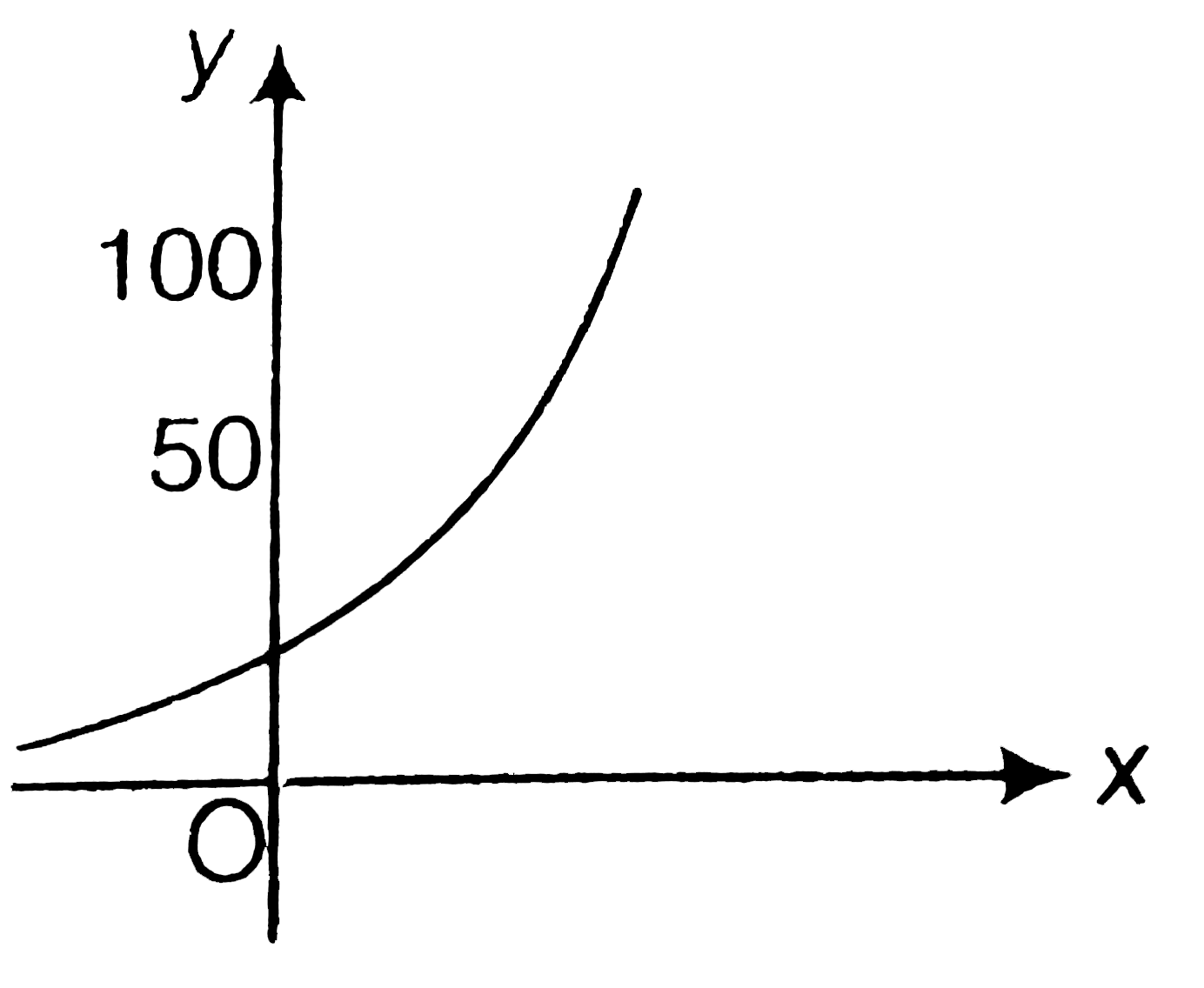
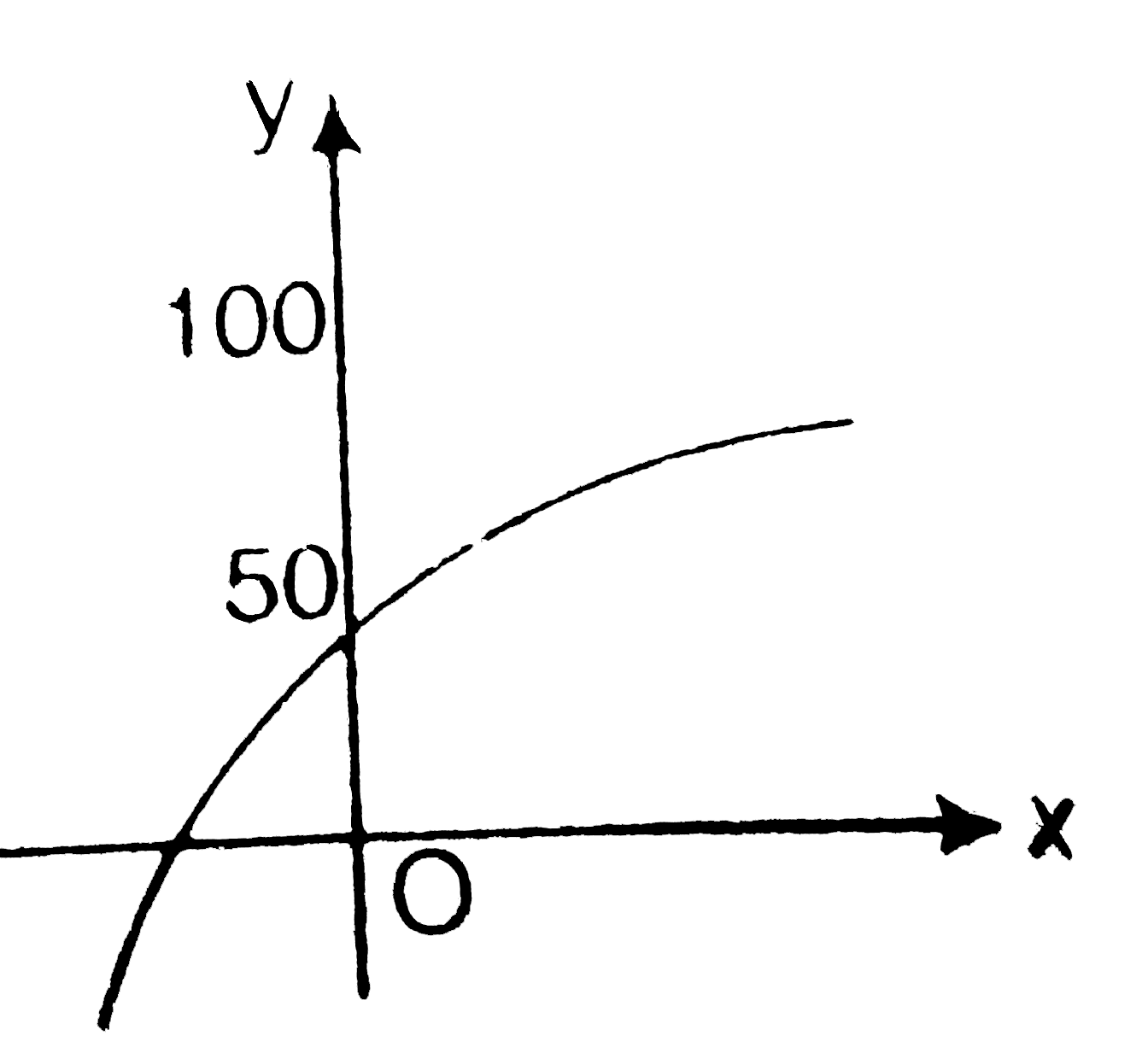
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
DIFFERENTIAL EQUATION
ARIHANT MATHS ENGLISH|Exercise Exercise (More Than One Correct Option Type Questions)|13 VideosDIFFERENTIAL EQUATION
ARIHANT MATHS ENGLISH|Exercise Exercise (Statement I And Ii Type Questions)|9 VideosDIFFERENTIAL EQUATION
ARIHANT MATHS ENGLISH|Exercise Exercise For Session 5|8 VideosDETERMINANTS
ARIHANT MATHS ENGLISH|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|18 VideosDIFFERENTIATION
ARIHANT MATHS ENGLISH|Exercise Exercise For Session 10|4 Videos
Similar Questions
Explore conceptually related problems
ARIHANT MATHS ENGLISH-DIFFERENTIAL EQUATION -Exercise (Single Option Correct Type Questions)
- If the differential equation of the family of curve given by y=Ax+Be^(...
Text Solution
|
- about to only mathematics
Text Solution
|
- The x-intercept of the tangent to a curve is equal to the ordinate of ...
Text Solution
|
- A function y = f(x) satisfies the condition f'(x) sin x + f(x) cos x=...
Text Solution
|
- A curve is such that the area of the region bounded by the co-ordinate...
Text Solution
|
- The value of the constant 'm' and 'c' for which y = mx + c is a soluti...
Text Solution
|
- Find the real value of m for which the substitution y=u^m will transfo...
Text Solution
|
- The solution of the differential equation, x^(2)dy/dxcos""(1)/(x)-ysi...
Text Solution
|
- A wet porous subtance in the open air loses its moisture at a rate pro...
Text Solution
|
- A curve C passes through origin and has the property that at each poin...
Text Solution
|
- A function y=f(x) satisfies (x+1)f^(')(x)-2(x^(2)+x)f(x) = e^(x^(2))/(...
Text Solution
|
- The curve with the property that the projection of the ordinate on the...
Text Solution
|
- The differential equation corresponding to the family of curves y=e^x ...
Text Solution
|
- The equation to the orthogonal trajectories of the system of parabolas...
Text Solution
|
- A function satisfying int0^1f(tx)dt=nf(x), where x>0 is
Text Solution
|
- The substituion y=z^(alpha) transforms the differential equation (x^(2...
Text Solution
|
- A curve passing through (2,3) and satisfying the differential equation...
Text Solution
|
- Which one of the following curves represents the solution of the initi...
Text Solution
|