Home
Class 12
MATHS
Let f (x) =1+ 1/2+ 1/3+ 1/4 + ……… + 1/n ...

Let `f (x) =1+ 1/2+ 1/3+ 1/4 + ……… + 1/n` such that `P (n) f (n+2) = P ( n) f (n) + q (n).` Where `P (n) Q(n)` are polynomials of least possible degree and `P (n)` has leading coefficient unity. Then match the following Column-I with Column-II.

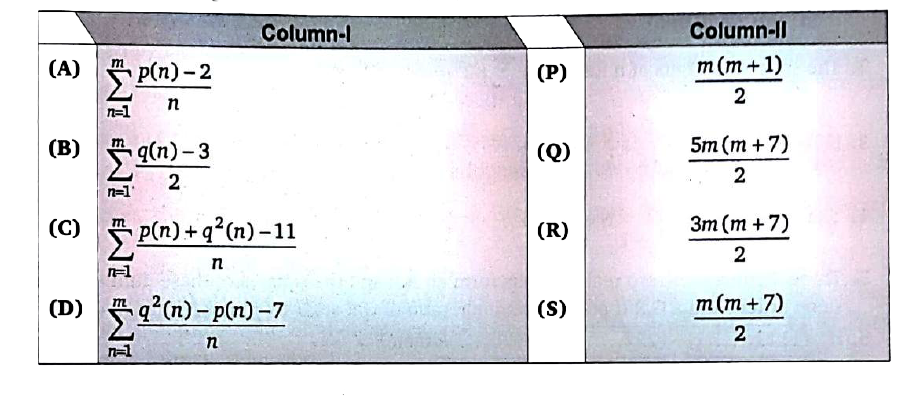
Text Solution

Verified by Experts

The correct Answer is:
`AtoS; BtoP; CtoQ; DtoR`
Promotional Banner

Topper's Solved these Questions

  • SEQUENCE AND SERIES

    VIKAS GUPTA (BLACK BOOK) ENGLISH|Exercise EXERCISE (SUBJECTIVE TYPE PROBLEMS)|21 Videos

  • SEQUENCE AND SERIES

    VIKAS GUPTA (BLACK BOOK) ENGLISH|Exercise EXERCISE (COMPREHENSION TYPE PROBLEMS)|16 Videos

  • QUADRATIC EQUATIONS

    VIKAS GUPTA (BLACK BOOK) ENGLISH|Exercise EXERCISE (SUBJECTIVE TYPE PROBLEMS)|45 Videos

  • SOLUTION OF TRIANGLES

    VIKAS GUPTA (BLACK BOOK) ENGLISH|Exercise Exercise-5 : Subjective Type Problems|11 Videos

Similar Questions

Explore conceptually related problems

If P(n ,5): P(n ,3)=2:1 find n

f(1)=1, n ge 1 f(n+1)=2f(n)+1 then f(n)=

Let f(n)=1+1/2+1/3++1/ndot Then f(1)+f(2)+f(3)++f(n) is equal to (a) nf(n)-1 (b) (n+1)f(n)-n (c) (n+1)f(n)+n (d) nf(n)+n

Let P(n): (2n+1) lt 2^(n) , then the smallest positive integer for which P(n) is true?

If the sum of n terms of an A.P. is n P +1/2n(n-1)Q , where P and Q are constants, find the common difference.

Let f : N rarr R be a function such that f(1) + 2f(2) + 3f(3) + ....+nf(n)= n(n+1) f(n) , for n ge 2 and f(1) = 1 then

Find n if : 2P( n,3) = P(n+1,3)

Prove the following: P(n , n)=P(n , n-1)

If f(x) =(p-x^n)^(1/n) , p >0 and n is a positive integer then f[f(x)] is equal to

Find n if : ""^(2n+1) P_(n-1) : ""^(2n-1) P_n = 3: 5