Home
Class 11
PHYSICS
A particle is projected up with initial ...

A particle is projected up with initial speed `u=10 m s^(-1)` from the top of a building at time `t=0`. At time `t=5 s` the particle strikes the ground. Find the height of the building.
.

Text Solution

Verified by Experts

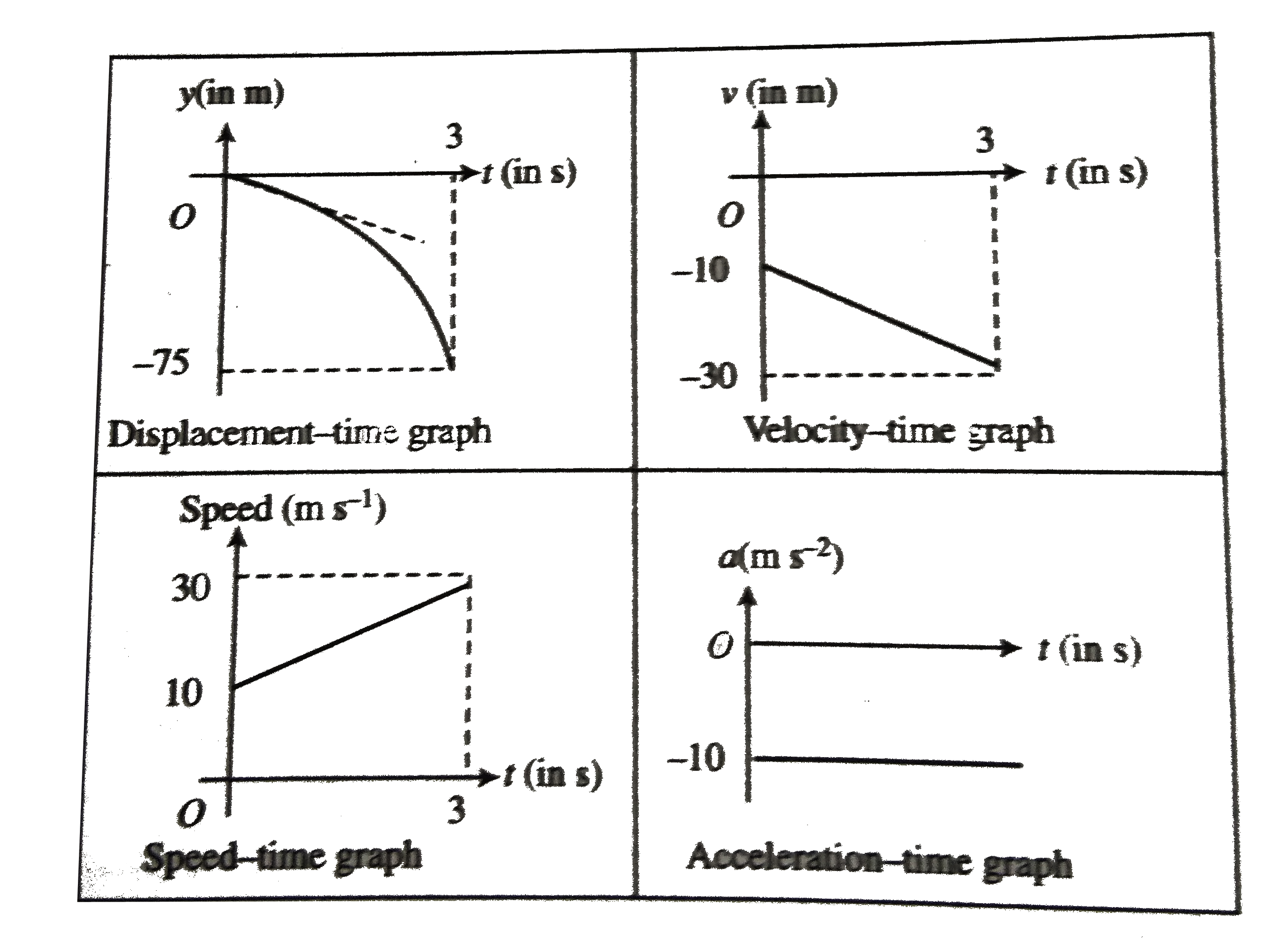
Taking oringin at the top of building and upward direction positive.
For particled A `u=+10 s^(-1) a=-10 m s^(-1)`
Using `y=ut+(1)/(2)at^(2)`
`=10t-(1)/(2) xx10xxt^2) =10t-5^(2)` ...(i)
Equation (i) is the equation of parabola open down The parabola passes origin when `y=0`. hence from
`0=10t-5t^(-2) rArr t=0,0 s`
For velocity-time relation, `v=u+at`
`v=10-10t`. (ii)
The relaation is straight line relation with negative slopen and positive intercept.
At maximum hetght, velocity of the particle is zero.
`0=10-10 t rArr t=1 s`
Maximum height from (i), `y_(max)=10xx1-5xx1^(2)=5 s s^(-1)`
It will reach ground wher `y=-100 m`
Using `i` again, `-74=10t-5t^(2) rArr (t-5)(t+3)=0`
When given `t=5 s`, i.e., the particle will hit ground at `t=5 s`.
Velocity at the time of hitting
Using (ii), `v=10-10xx5=40 m s^(-1)`
For speed-time relation, the speed is always positive the mirror-image of velocity-time relation on positive side.
For drawing acceleration-time graph we have taken downward direction as negative and acceleration is constant throughout the motion of the praticle, i.e. `-10 m s^-(2)` Hence, acceleration time graph will be straight line parallel with time axis and below the time axis.
.
d. For particle B:`u=-10 m s^(-1) a=-20 m s^(-2)`
Displacement-time relation,
`y=-10t-(1)/(2)xxt^(2)=-10t^(2)` ...(iii)`
It is a parabla open down and it passes through origin. The particel will reach ground when `y=-75 m`
From (iii) `=-10t-5t^(2)`
or `t^(2)+2t-15=0 rArr t=3 s`
The velocity of the particle in relation with time
`v=0-10t rArr v=10t` ...(iv)
This is a straight line with negative slope and passing through origin. The particle reaches fround at `t=3 s`, velocity of the particle when it hits ground is
`v=-10xx3=-30 m s^(-1)`
.
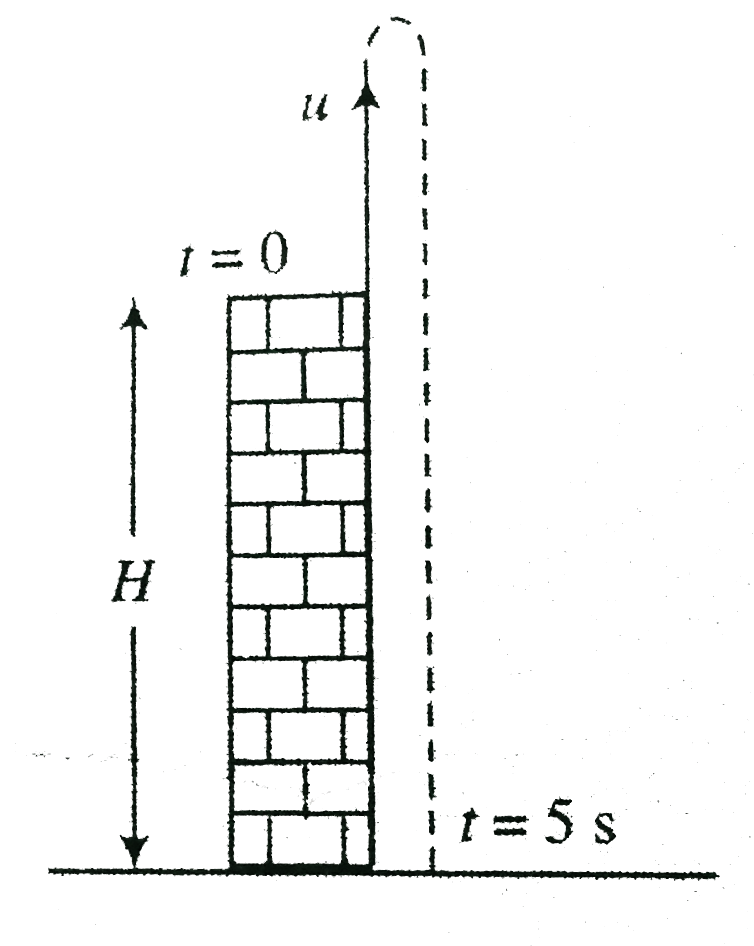
For particle C: `u=0. a=-10 m s^(-2)`
Using `y=ut+(1)/(2)at^(2)`
`=0-(1)/(2)(-10)t^(2)=-5t^(2)`
It is a parabola open down and it passes through origin.
For velocity-time relation `vec v=vec u+vec at`
`v=0-10 t =-10t` ..(vi)
Straight line with negative slope passes through origion.
It will reach round at `y=-75 m`
`-75=-5t^(2) rArr t=sqrt15 s`
Velocity at the time when it reaches ground `v=-10sqrt15 s`.
.
Promotional Banner

Topper's Solved these Questions

  • KINEMATICS-1

    CENGAGE PHYSICS ENGLISH|Exercise Solved Examples|9 Videos

  • KINEMATICS-1

    CENGAGE PHYSICS ENGLISH|Exercise Exercise 4.1|17 Videos

  • GRAVITATION

    CENGAGE PHYSICS ENGLISH|Exercise INTEGER_TYPE|1 Videos

  • KINEMATICS-2

    CENGAGE PHYSICS ENGLISH|Exercise Exercise Integer|9 Videos

Similar Questions

Explore conceptually related problems

A particle is projected up with initial speed u=10 m s^(-1) from the top of a bitlding at time t=0 . At time t=5 s the particle strikes the fround. Find the height of the building. .

A particle is projected from the ground at an angle such that it just clears the top of a polar after t_1 time its path. It takes further t_2 time to reach the ground. What is the height of the pole ?

A stone is thrown downwards with velocity 10 m/s from the roof of a builng and it reaches the ground with speed 40 m/s. the height of the building would be

A particle is projected with initial velocity u = 10 m//s from a point ( 10m, 0m, 0m ) m along z-axis. At the same time , another particle was also projected with velocity v ( hat(i) - hat(j) + hat( k)) m//s from ( 0m, 10m, 0m). It is given that they collide at some point in the space . Then find the value of v. [ vec(g) = 10 m//s^(2) ( - hat(k))]

A ball is thrown downwards with a speed of 20 m s^(-1) , from the top of a building 150 m high and simultaneously another ball is thrown vertically upwards with a speed of 30 m s^(-1) from the foot to the building . Find the time after which both the balls will meet. (g=10 m s^(-2)) .

A particle A is projected with an initial velocity of 60 m//s at an angle 30^@ to the horizontal. At the same time a second particle B is projected in opposite direction with initial speed of 50 m//s from a point at a distance of 100 m from A. If the particles collide in air, find (a)the angle of projection alpha of particle B, (b) time when the collision takes place and (c) the distance of P from A, where collision occurs. (g= 10 m//s^2)

A particle is projected horizontally with a speed u from the top of plane inclined at an angle theta with the horizontal. How far from the point of projection will the particle strike the plane ?

A particle is projected vertically up from the top of a tower with velocity 10 m//s . It reaches the ground in 5s. Find - (a) Height of tower (b) Striking velocity of particle at ground (c ) Distance traversed by particle. (d) Average speed & average velocity of particle.

A particle moves vertically with an upwards initial speed v_0 = 10.5 ms^(-1). If its acceleration varies with time as shown in a-t graph in figure, find the velocity of the particles at t = 4s.

A particle is projected from a tower of height 25 m with velocity 20sqrt(2)m//s at 45^@ . (a) Find the time when particle strikes with ground. (b) The horizontal distance from the foot of tower where it strikes. (c) Also find the velocity at the time of collision.