Text Solution
Verified by Experts
Topper's Solved these Questions
KINEMATICS-1
CENGAGE PHYSICS ENGLISH|Exercise Exercise 4.3|15 VideosKINEMATICS-1
CENGAGE PHYSICS ENGLISH|Exercise Exercise 4.4|16 VideosKINEMATICS-1
CENGAGE PHYSICS ENGLISH|Exercise Exercise 4.1|17 VideosGRAVITATION
CENGAGE PHYSICS ENGLISH|Exercise INTEGER_TYPE|1 VideosKINEMATICS-2
CENGAGE PHYSICS ENGLISH|Exercise Exercise Integer|9 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-KINEMATICS-1-Exercise 4.2
- a. Mark the follllowing statements as true offalse. i. A ball thrown...
Text Solution
|
- A ball thrown up from the ground reaches a maximum height of 20 m Find...
Text Solution
|
- A body is projected from the bottom of a smooth inclined place with a ...
Text Solution
|
- A ball is dropped from an elevator at an altitude of 200 m (Fig.4. 39)...
Text Solution
|
- A particle is projected vertically upwards. Prove that it will be at t...
Text Solution
|
- A balloon rises from rest on the ground with constant acceleration g/8...
Text Solution
|
- A parachutist after bailing out falls 50m without friction. When parac...
Text Solution
|
- A ball is dropped from the top of a tower of herght (h). It covers a d...
Text Solution
|
- When a ball is thrown up, it reaches a maximum height (h) travelling (...
Text Solution
|
- You are on the roof of the physics building, 46.0 m above the ground ....
Text Solution
|
- A ball (A) is thrown straight up from the edge of the roof of a buildi...
Text Solution
|
- Two particles are simultaneously released from points A and D as shown...
Text Solution
|
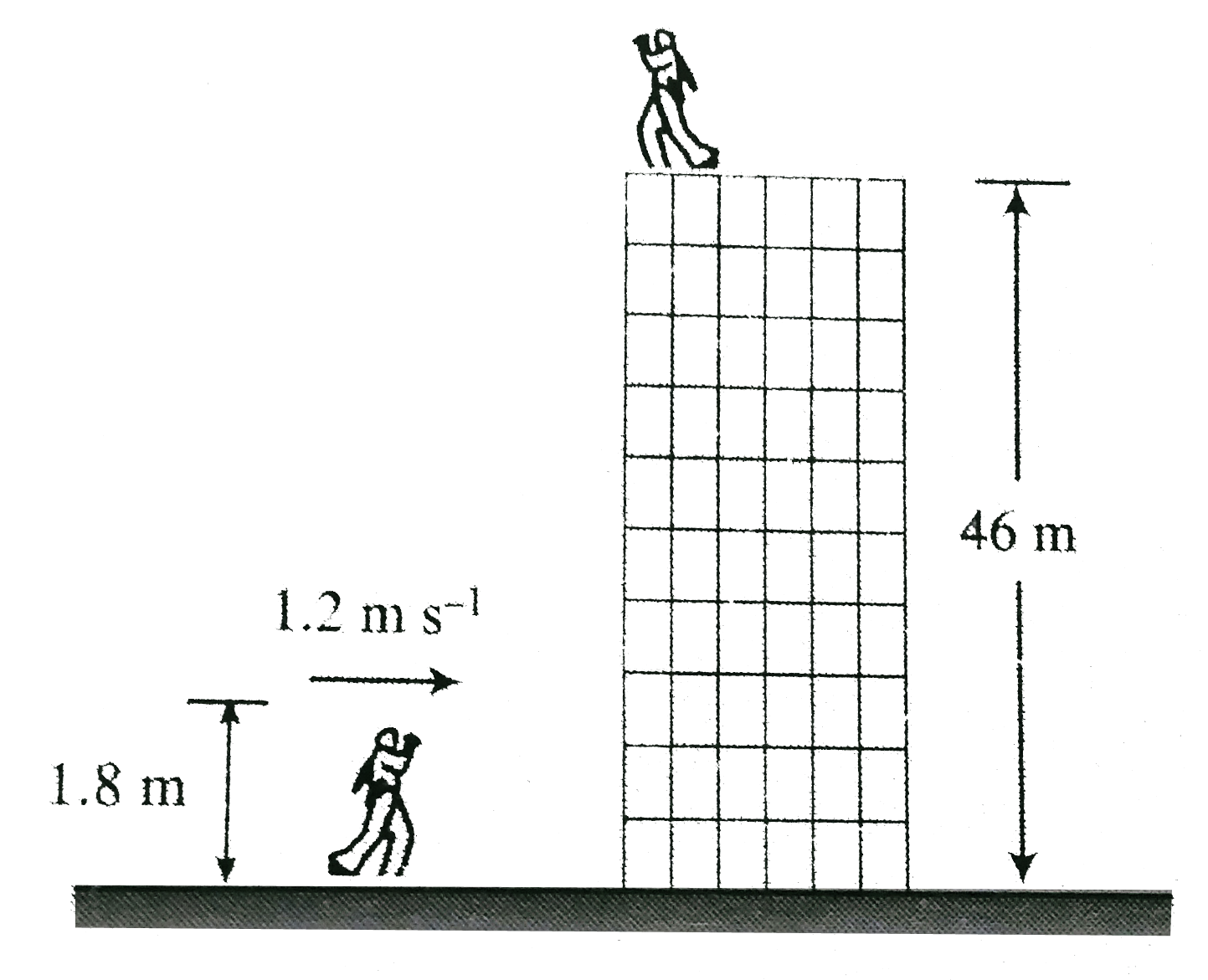 .
.