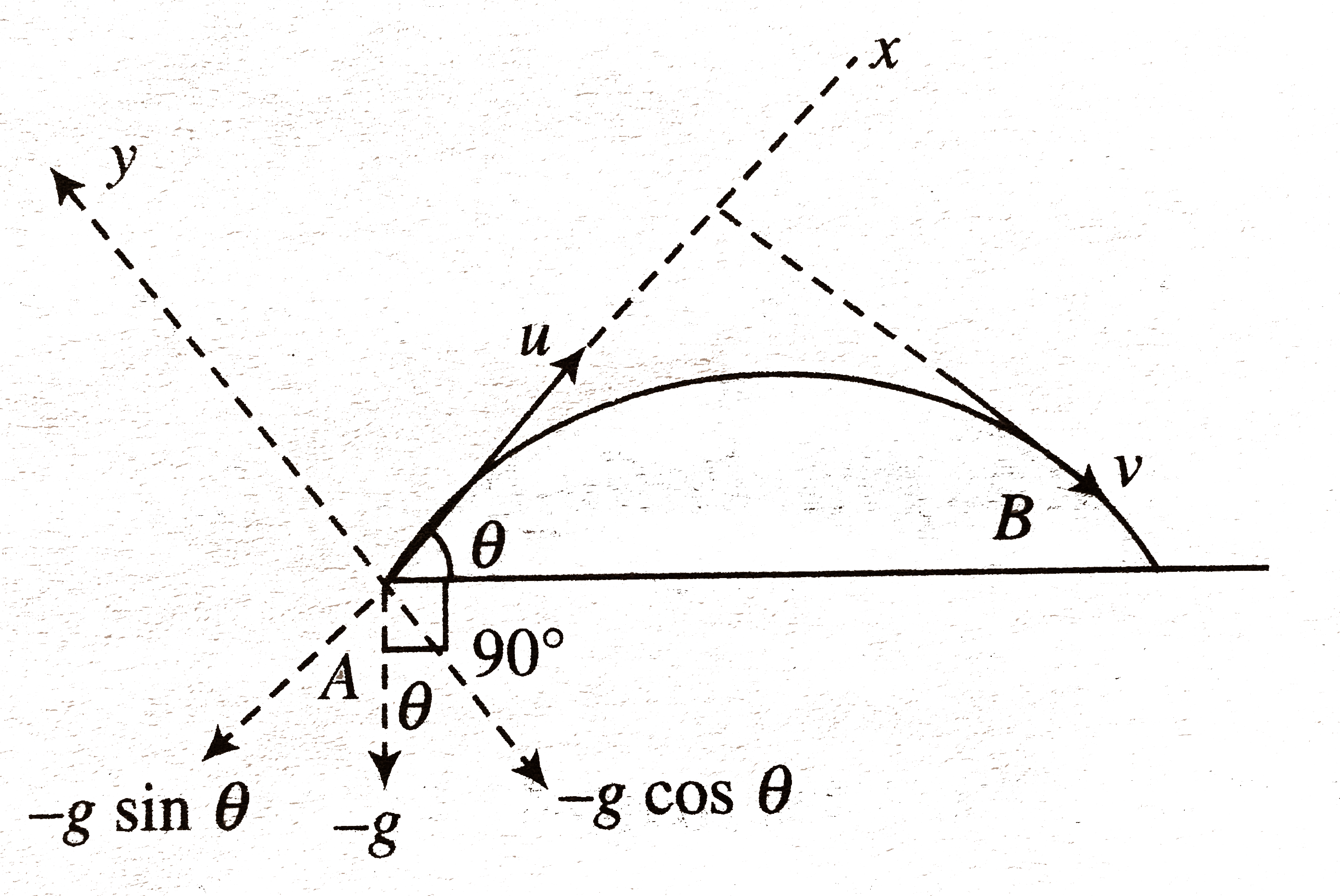Method 1 : Using properties of projectile motion
As we have to calculate the time between two positions `A and B` where the final direction of movement is perpendicular to the initial direction of movement. So for our own comfortability, we can choose the initial direction of motion as x - axis. Also let us assume the velocity at position `B` to be `v`.
Now analyzing motion in x - and y - direction, we have
`u_x = u , u_y = 0`
`a_x = -g sin theta , a_y = -g cos theta`
Here we can the following formula `v = u + at` in x - direction.
As we have the values of initial velocity, final velocity, and acceleration we can find `t`. Therefore,
`v_x = u_x + a_x t`
At position `B, v_x = 0`, as the fianl velocity is equal to the y - component of velocity. Therefore,
`0 = u - g sin theta. t`
Thus, `t = (u)/(g sin theta)` which is the required time to travel.
Method 2 : Using vectors
As `u and v` both are perpendicular to each other. We can use the orthogonality property of dot product, i.,e., if two vetor are perpendicular to each other their dot product is zero, in order to find out the time of travel to the desired position. So,
so, `vec u . vec v = 0 rArr vec u .(vec u + vec a t) = 0 rArr vec u . vec u + vec u. vec a t = 0`
`rArr u^2 + ug cos (90^@ + theta) t = 0`
[because angle between `u` and `g is 90^@ + theta` as from (Fig)]
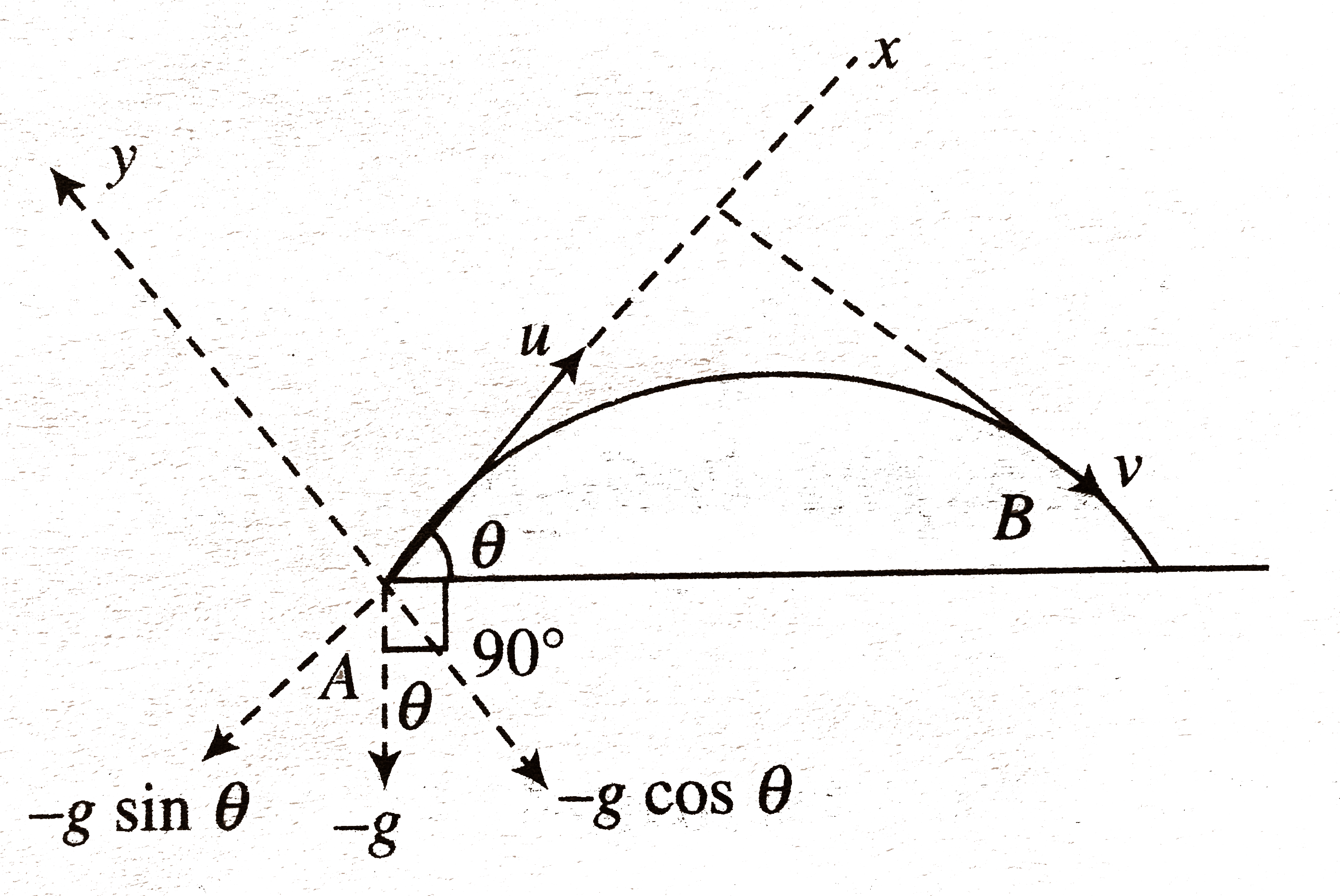
`u^2 + u.g (-sin theta) t = 0 . t = 0`
So, `t = (u)/(g sin theta)` is the desired time.
To find out the velocity we can use the same relation as used in this question. But as at final position (considered) only the y - component of velocity is present, so we need to use the same relation in y - direction.
`v_y = u_y + a_g t`
`rArr v = 0 -g. cos theta t`
=`- g cos theta (u)/(g sin theta) = - u cot theta` is the velocity at position `B`.
.
Method 3 : If the initial velocity `u` and velocity at time `t` are perpendicular, then the final velocity will be at an angle `theta` with the vertical.
The horizontal component of velocity is unchanged throughout the motion . Therefore,
`u cos theta = v sin theta`
or `v = u cot theta`
THe vertical component of velocity after time `t = -v cos theta`.
From the equation, `v_y = u sin theta - g t -v cos theta = u sin theta - g t`
`t = (u sin theta + v cos theta)/(g) = (u sin theta + u cot theta cos theta)/(g)`
=`(u)/(g)[(sin^2 theta + cos^2 theta)/(sin theta)] = (u)/(g) cosec theta`
Method 4 : The slope of trajectory at the point of projection, `m_1 = tan theta`
Slope of trajectory after time `t`,
`m_2 = (d y)/(d x) = (d y//d t)/(d x//d t) =(v_y)/v_x = (u sin theta - g t)/( u cos theta)`
Slopes are perpendicular, `((u sin theta - g t)/(u cos theta)) (tan theta) = - 1`
or `t = (u)/(g sin theta)`.