Two identical buggies move one after the other due to inertia (without friction) with the same velocity `v_0`. A man of mass m rides the rear buggy. At a certain moment the man jumps into the front buggy with a velocity u relative to his buggy. Knowing that the mass of each buggy is equal to M, find the velocities with which the buggies will move after that.

Explanation

If we take rear buggy `+` man as system. There is no external force acting on system is horizontal direction. Hence linear momentum of the system should be conserved. Let velocity of rear buggy just after jumping be `vecV_(r)`, the velocity of man just after jumping will be `(vecV_(r)+vecu)`

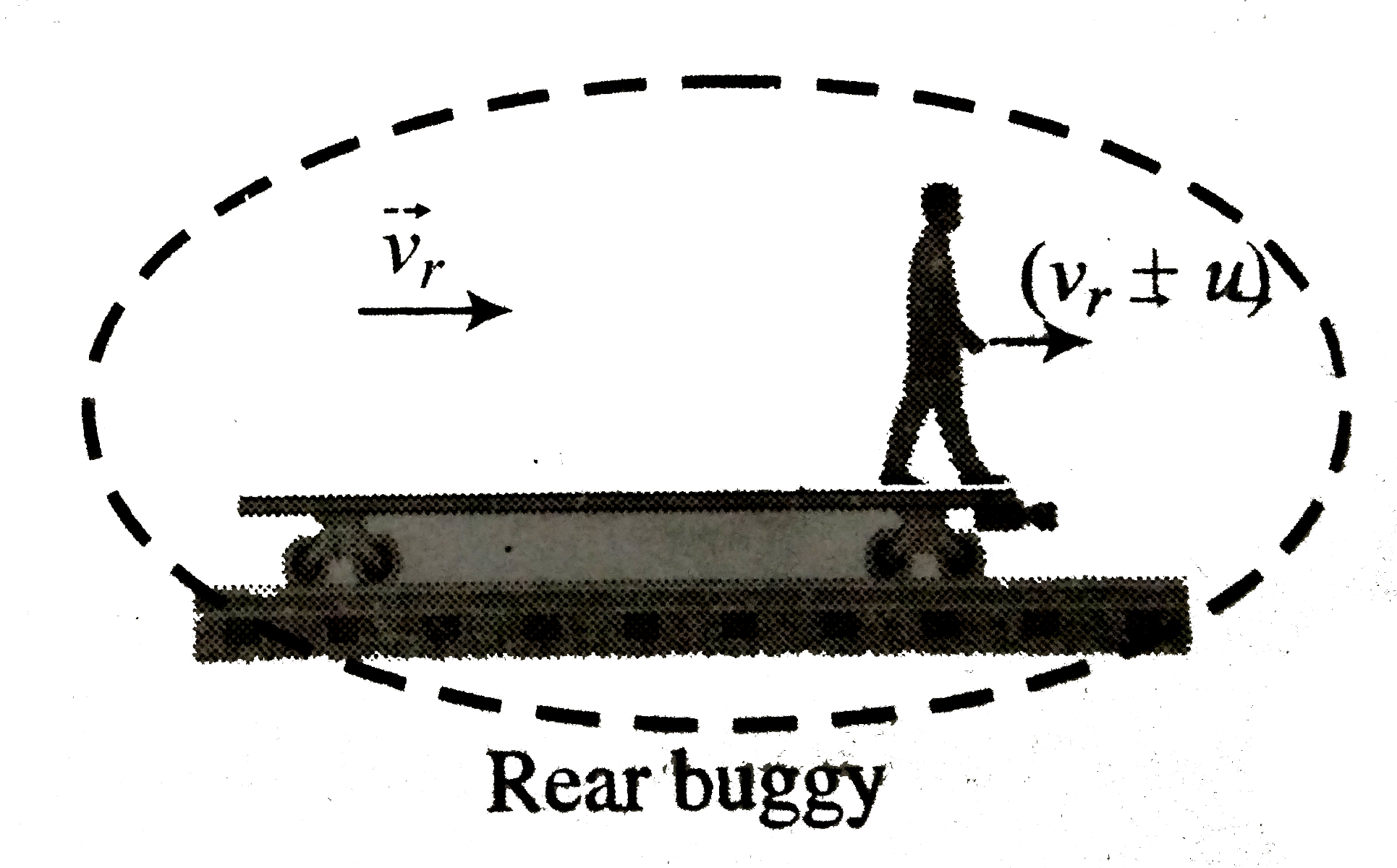
`vecp_(i)=(M+m)vecV_(0)`
`vecp_(f)=MvecV_(r)+m(vecV_(r)+vecu)` and `vecp_(i)=vecp_(f)`
`implies(M+m)vecV_(0)=MvecV_(r)+m(vecV_(r)+vecu)`
`vecV_(r)=vecV_(0)-(mvecu)/((M+m))`..............i

Now considering front buggy andn man as system, and again conserving linear momentum in horizontal direction.
`M_(0)vecV_(0)+m(vecu+vecV_(r))=(m+M)vecV_(r)`
`MvecV_(0)=m(vecu+vecV_(0)-(muvecu)/((M+m)))=(m+M)vecV_(f)`
`impliesvecV_(f)=vecV_(0)=(Mmvecu)/((M+m)^(2))`