A smooth wedge of mass `M` rests on a smooth horizontal surface. A block of mass `m` is projected from its lowermost point with velocity `v_(0)`. What is the maximum height reached by the block?
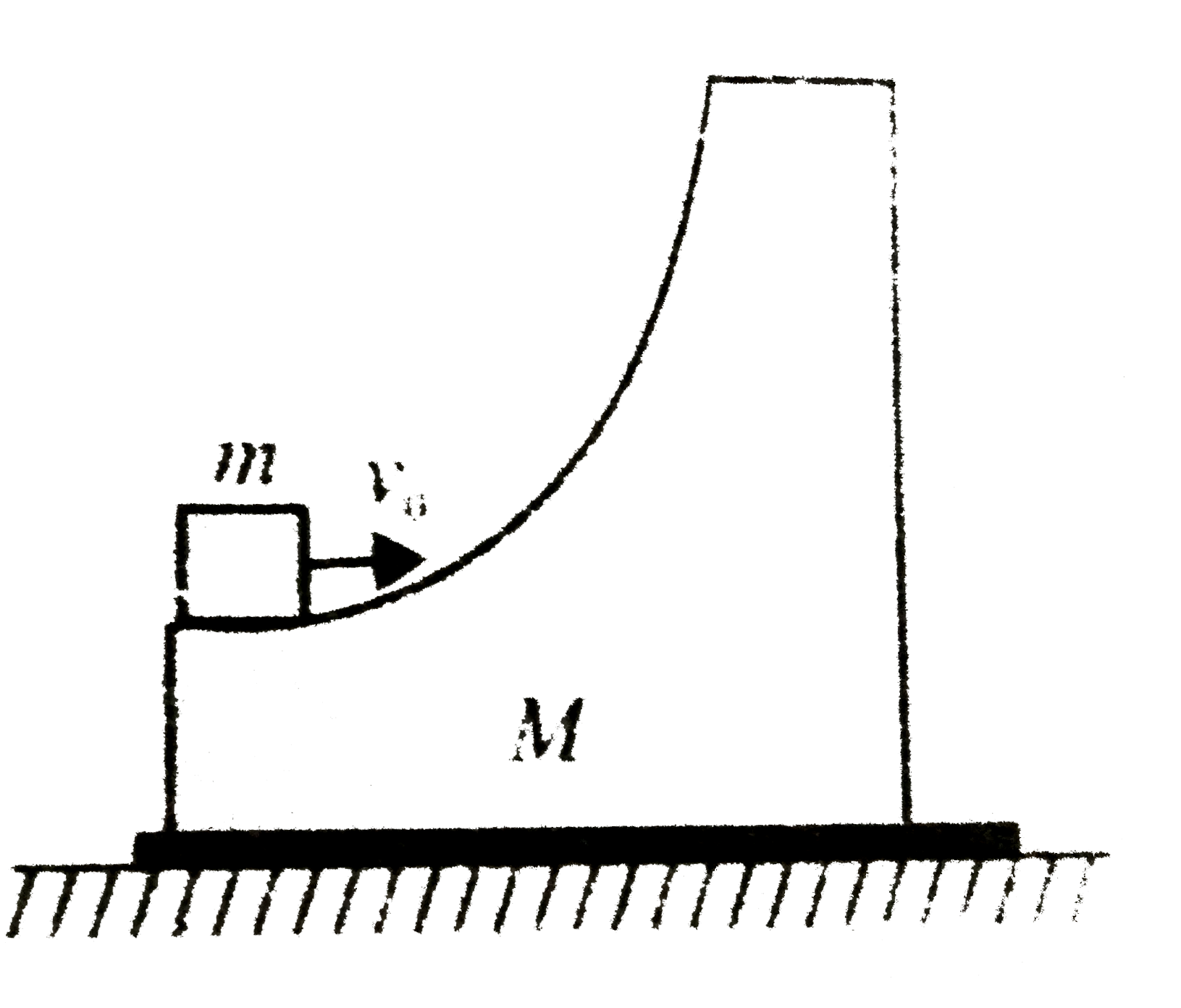
A smooth wedge of mass `M` rests on a smooth horizontal surface. A block of mass `m` is projected from its lowermost point with velocity `v_(0)`. What is the maximum height reached by the block?


Text Solution
Verified by Experts
Method 1 (Ground frame method)
At the maximum height, both `m_(1)` and `m_(2)` have same velocity as the relative sliding between them stops. Since no external force acts horizontally, linear momentum is conserved in horizontal direction
`(vecp_(x))_(f)=(vecp_(x))_(i)`
where `vecp_(x_(i))=m_(1)v_(0)hati` and `vecp_(x_(f))=(m_(1)+m_(2))vhati`
Then we have `(m_(1)+m_(2))v=m_(1)v_(0)`
WE theorem `W_(ext)+W_("int")=/_\K`
where `W_("ext")=-m_(1)gh, W_("int")=W_("contact")=0, `
and `/_\ K=[1/2(m_(1)+m_(2))v^(2)-(m_(1)v_0^(2))/2]`
This gives `-m_(1)gh=1/2(m_(1)+m_(2))v^(2)-(m_(1)v_(0)^(2))/2`........ii
Sustituting `v` from eqn i and eqn ii we have
`h=v_(0)^(2)/(2(1+m_(1)/m_(2))g)`
Method 2: (Work energy theorem from centre of mass frame)
The block attains a maximum height when the final relative velociyt `v_(rel)` between block and wedge becomes zero.
that mean `(v_(ref))=0`.
The initial relative velocity betwen block and wedge is given as
`(v_(ref))_(i)=v_(0)`
Substituting `(v_(ref)_(f)=0` and `(v_(rel))_(i)=v_(0)` in the formula.
`/_\K'=1/2mu[(v_(rel)_(f)^(2)-(v_(rel))_(i)^(2)]`
we have `/_\K'=-1/2muv_(0)^(2)`
while ascending through a height `h` (say) the external force, that is the earth's gravity does work on the block `m_(1)` which can be given as:
`W_(ext)(=W_("gravity"))=-m_(1)gh`
The internal (constraint) forces (normal reactions) between `m_(1)` and `m_(2)` as a whole do not performe work, `W_(int)=0`
Finally, putting `/_\K'=-1/2muv_(0)^(2), W_(ext)=-m_(1)gh` and `W_("int")=0` in
We theorem `W_(ext)+W_("int")=/_\K'`
we have `-m_(1)gh+0=-1/2muv_(0)^(2)`
`where mu=(m_(1)m_(1))/(m_(1)+m_(2))`
This gives `h=v_(0)^(2)/(2(1+m_(1)/m_(2))g)`
At the maximum height, both `m_(1)` and `m_(2)` have same velocity as the relative sliding between them stops. Since no external force acts horizontally, linear momentum is conserved in horizontal direction
`(vecp_(x))_(f)=(vecp_(x))_(i)`
where `vecp_(x_(i))=m_(1)v_(0)hati` and `vecp_(x_(f))=(m_(1)+m_(2))vhati`
Then we have `(m_(1)+m_(2))v=m_(1)v_(0)`
WE theorem `W_(ext)+W_("int")=/_\K`
where `W_("ext")=-m_(1)gh, W_("int")=W_("contact")=0, `
and `/_\ K=[1/2(m_(1)+m_(2))v^(2)-(m_(1)v_0^(2))/2]`
This gives `-m_(1)gh=1/2(m_(1)+m_(2))v^(2)-(m_(1)v_(0)^(2))/2`........ii
Sustituting `v` from eqn i and eqn ii we have
`h=v_(0)^(2)/(2(1+m_(1)/m_(2))g)`
Method 2: (Work energy theorem from centre of mass frame)
The block attains a maximum height when the final relative velociyt `v_(rel)` between block and wedge becomes zero.
that mean `(v_(ref))=0`.
The initial relative velocity betwen block and wedge is given as
`(v_(ref))_(i)=v_(0)`
Substituting `(v_(ref)_(f)=0` and `(v_(rel))_(i)=v_(0)` in the formula.
`/_\K'=1/2mu[(v_(rel)_(f)^(2)-(v_(rel))_(i)^(2)]`
we have `/_\K'=-1/2muv_(0)^(2)`
while ascending through a height `h` (say) the external force, that is the earth's gravity does work on the block `m_(1)` which can be given as:
`W_(ext)(=W_("gravity"))=-m_(1)gh`
The internal (constraint) forces (normal reactions) between `m_(1)` and `m_(2)` as a whole do not performe work, `W_(int)=0`
Finally, putting `/_\K'=-1/2muv_(0)^(2), W_(ext)=-m_(1)gh` and `W_("int")=0` in
We theorem `W_(ext)+W_("int")=/_\K'`
we have `-m_(1)gh+0=-1/2muv_(0)^(2)`
`where mu=(m_(1)m_(1))/(m_(1)+m_(2))`
This gives `h=v_(0)^(2)/(2(1+m_(1)/m_(2))g)`
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
A horizontal force F pushes wedge of mass M on a smooth horizontal surface. A block of mass m is stationary to the wedge, then:
A smooth wedge of mass M is pushed with an acceleration a=gtantheta and a block of mass m is projected down the slant with a velocity v relative to the wedge. Q. The time taken by the block to reach the ground is:
A wedge of mass 4m is initially at rest on frictionles horizotnal surface. A small block of mass m moving with speed v_(0) and climbs on wedge. Find maximum height achieved by block
A long block A of mass M is at rest on a smooth horizontal surface.A small block B of mass M//2 is placed on A at one end and projected along A with some veklocity v.The coefficient of friction between the block is mu then , the accelerations of blocks A and B before reaching a common velocity will be respectively
Figure shows a block A of mass 6 m having a smooth semicircular groove of radius a placed on a smooth horizontal surface. A block B of mass m is released from a position in groove where its radius is horizontal. Find the speed of the bigger block when the smaller block reaches its bottom most position.
A smooth wedge of mass M is pushed with an acceleration a=gtantheta and a block of mass m is projected down the slant with a velocity v relative to the wedge. The horizontal force applied on the wedge is:
A smooth wedge of mass M is pushed with an acceleration a=g tantheta and a block of mass m is projected down the slant with a velocity v relative to the wedge. Q. The normal reaction between wedge and block is:
A smooth wedge of mass M is pushed with an acceleration a=gtantheta and a block of mass m is projected down the slant with a velocity v relative to the wedge. Q. The normal reaction offered by ground to the wedge is:
A wedge shaped block A' of mass M is at rest on a smooth horizontal surface. A small block 'B' of mass 'm' placed at the top edge of inclined plane of length 'l' as shown in the figure. By the time, the block 'B' reaches the bottom end, the wedge A moves a distance of:
A wedge of mass M = 2m rests on a smooth horizontal plane. A small block of mass m rests over it at left end A as shown in figure. A sharp impulse is applied on the block, due to which it starts moving to the right with velocity v_(0) = 6 ms^(-1) . At highest point of its trajectory, the block collides with a particle of same mass m moving vertically downwards with velocity v = 2 ms^(-1) and gets stuck with it. If the combined body lands at the end point A of body of mass M, calculate length l . Neglect friction (g = 10 ms^(-2)) .