A flatcar of mass `m_0` starts moving to the right due to a constant horizontal force F(figure). Sand spills on the flatcar from a stationary hopper. The velocity of loading is constant and equal to `mukg//s`. Find the time dependence of the velocity and the acceleration of the flatcar in the process of loading. The friction is negligibly small.

Explanation

Initial velocity of the flat car is zero. Let `v` be its velocity at time `t` and `m` be its mass at that instant. Then

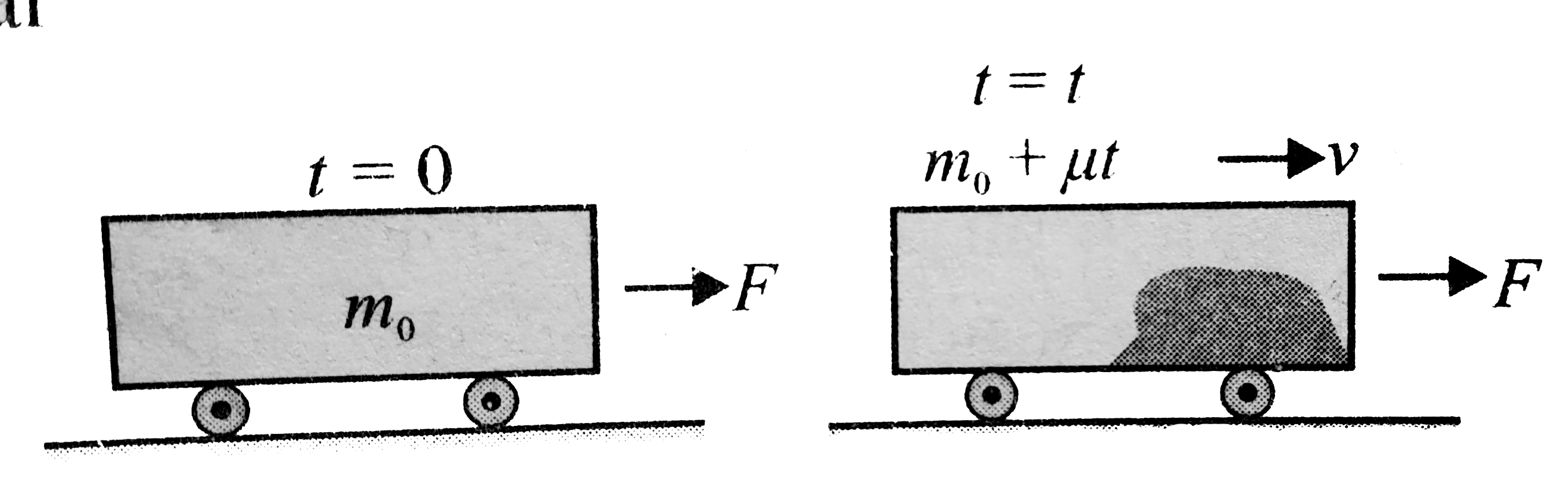
At `t=0,v=0` and `m=m_(0)`
At `t=t,v=v` and `m=m_(0)+mut`
Here, `v_(r)=u-v=0-v=-v`
here `u` is the velocity of mass being added in the horizontal direction which is zero.
`(dm)/(dt)=mu`
Apply `F+v_(rel)=(dm)/(dt)=(mdv)/(dt)` we get
`F+(-v)mu=(m_(0)+mut)(dv)/(dt)`
or `int_(0)^(v)(dv)/(F-muV)=int_(0)^(t)(dt)/(m_(0)+mut)`
`implies-1/mu[(n(F-muv)]_(0)^(v)1/(-mu)[In(m_(0)+mut)]_(0)^(t)`
`impliesIn(F/(F-muv))=(n((m_(0)+mut)/m_(0)))`
`implies F/(F-muV)=(m_(0)+mut)/m_(0)`
or `v=(Ft)/(m_(0)+mut)` ..........ii
from eqn i
`a=(F-muv)/m=((F-(Fmut)/(m_(0)+mut))/(mu_(0)+mut))`
or `a=(Fm_(0))/((m_(0)+mut)^(2))`