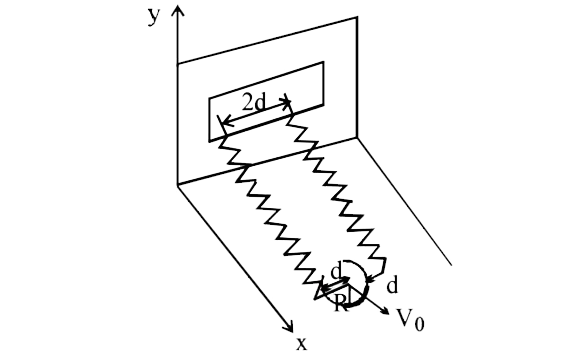
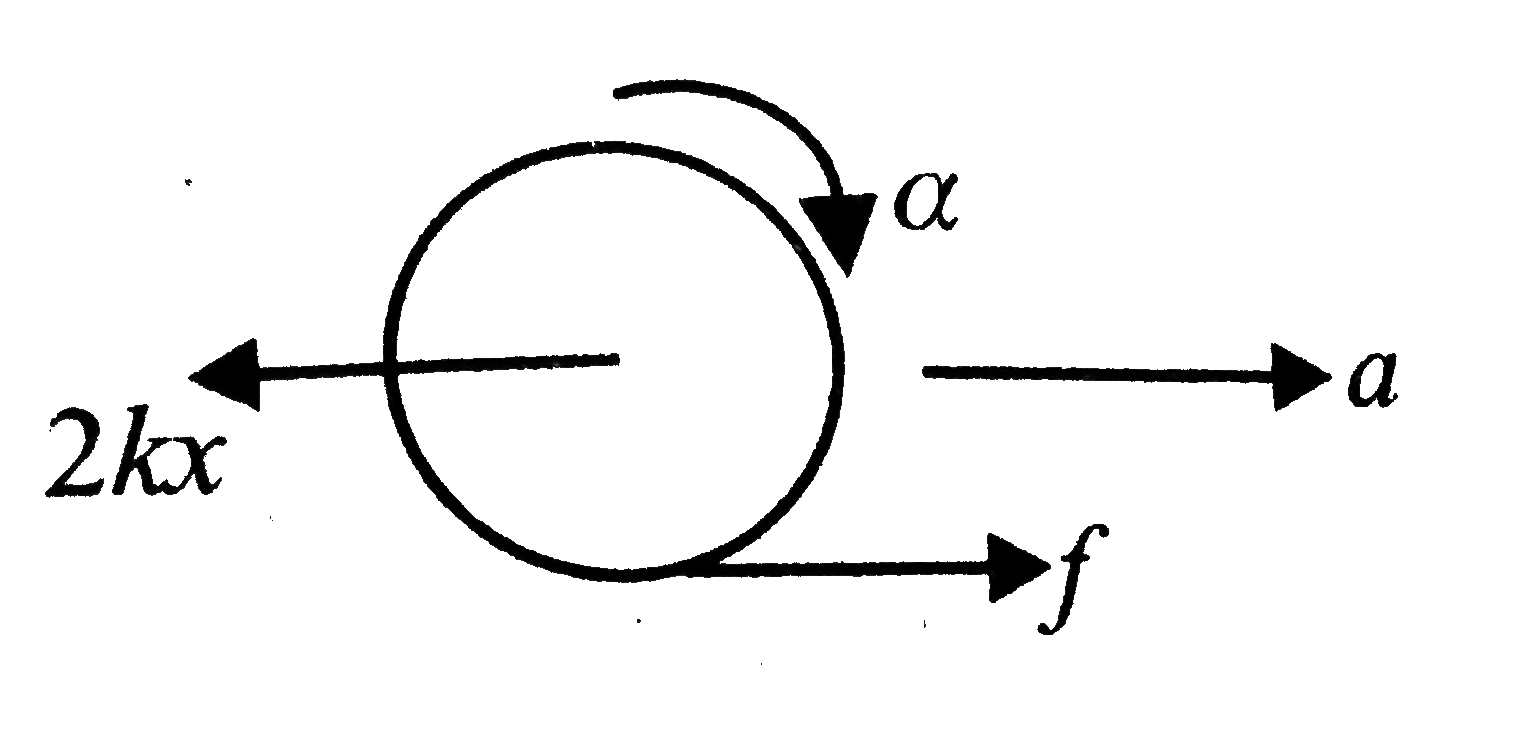
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-RIGID BODY DYNAMICS 2-LC_TYPE
- Two discs A and B are mounted co-axially one vertical axle. The discs ...
Text Solution
|
- Two discs A and B are mounted coaxiallay on a vertical axle. The discs...
Text Solution
|
- Two discs A and B are mounted coaxially ona vertical axle. The discs h...
Text Solution
|
- A uniform thin cylindrical disk of mass M and radius R is attaached to...
Text Solution
|
- A uniform thin cylindrical disk of mass M and radius R is attaached to...
Text Solution
|
- A uniform thin cylindrical disk of mass M and radius R is attaached to...
Text Solution
|
- The general motion of a rigid body can be considered to be a combinati...
Text Solution
|
- The general motion of a rigid body can be considered to be a combinati...
Text Solution
|