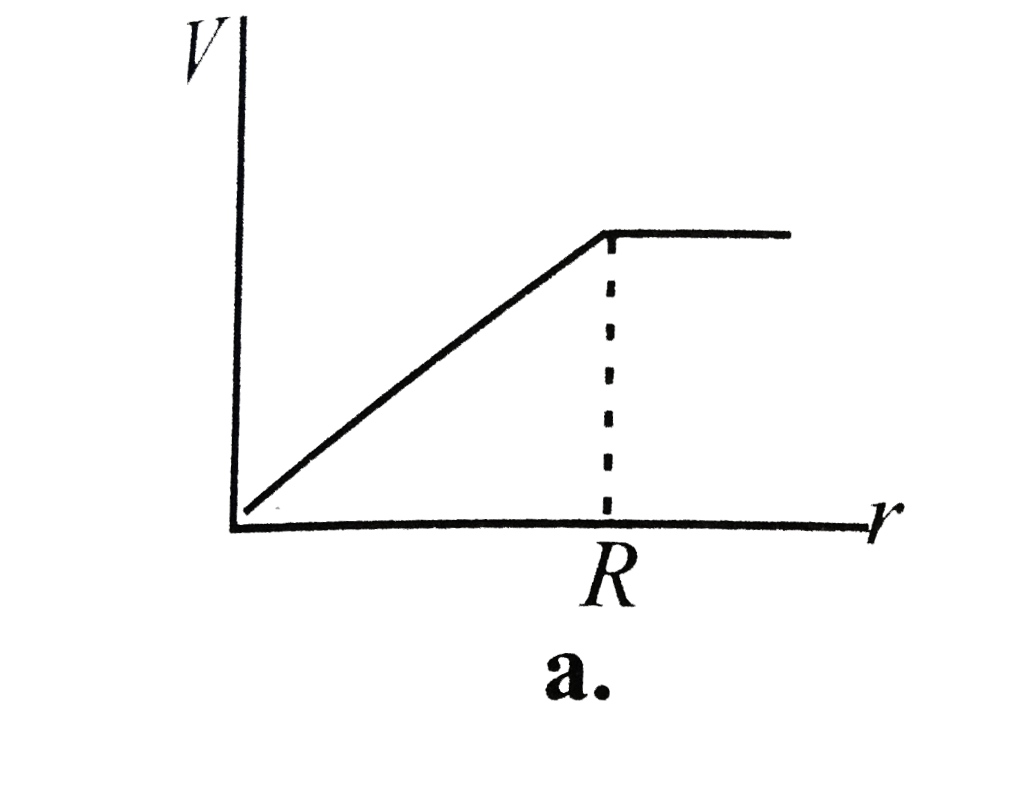
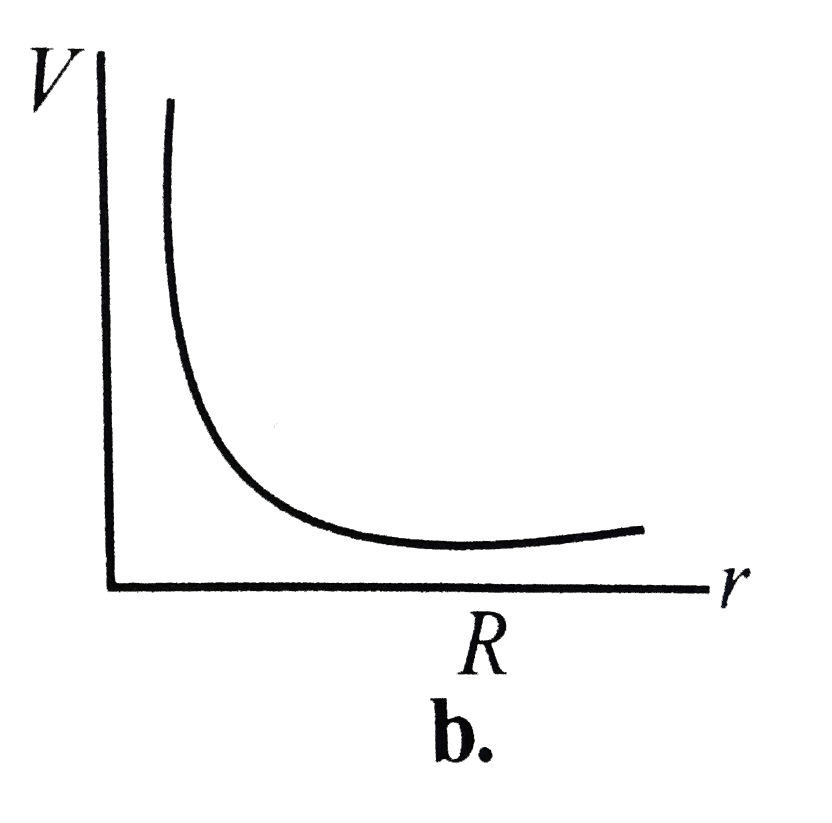
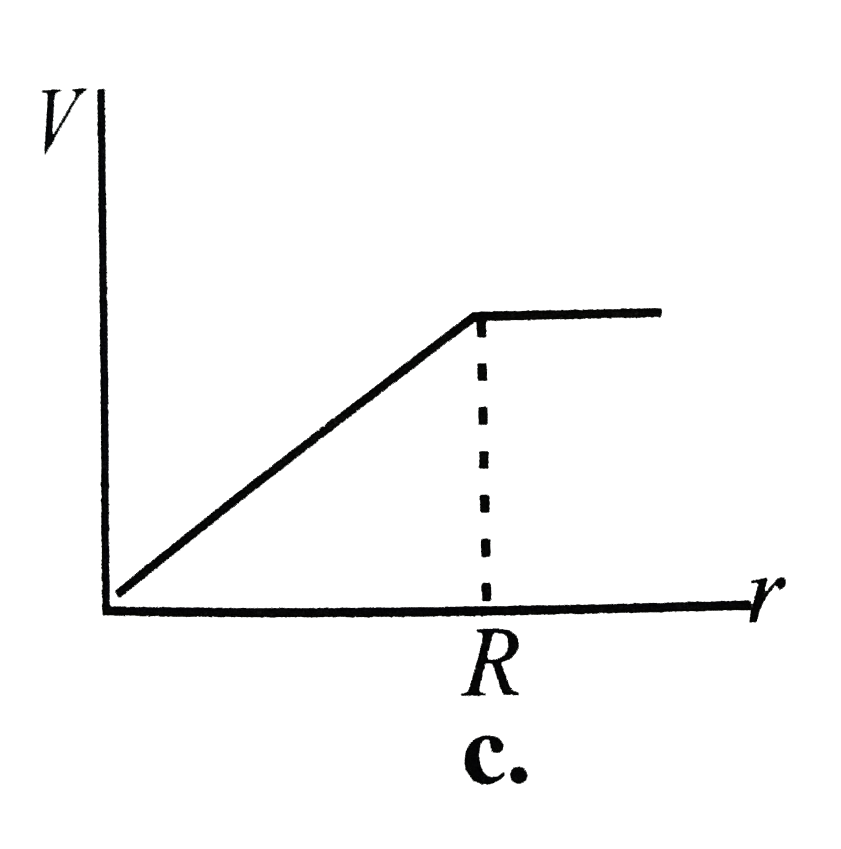
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
GRAVITATION
CENGAGE PHYSICS ENGLISH|Exercise MCQ_TYPE|4 VideosGRAVITATION
CENGAGE PHYSICS ENGLISH|Exercise AR_TYPE|1 VideosGRAVITATION
CENGAGE PHYSICS ENGLISH|Exercise True/False|1 VideosFLUID MECHANICS
CENGAGE PHYSICS ENGLISH|Exercise INTEGER_TYPE|1 VideosKINEMATICS-1
CENGAGE PHYSICS ENGLISH|Exercise Integer|9 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-GRAVITATION-SCQ_TYPE
- If the radius of the earth were to shrink by 1%, its mass remaining th...
Text Solution
|
- If g be the acceleration due to gravity of the earth's surface, the ga...
Text Solution
|
- A small planet is revolving around a very massive star in a circular o...
Text Solution
|
- If the distance between the earth and the sun were reduced to half its...
Text Solution
|
- A satellite S is moving in an elliptical orbit around the earth. The m...
Text Solution
|
- A simple pendulum has a time period T(1) when on the earth's surface a...
Text Solution
|
- The geostationalry orbit oif the earth is at a distance of about 36000...
Text Solution
|
- A system of binary stars of mass m(A) and m(B) are moving in circular ...
Text Solution
|
- A spherically symmetric gravitational system of particles has a mass d...
Text Solution
|
- A thin uniform disc (see figure) of mass M has outer radius 4R and in...
Text Solution
|
- A satellite is moving with a constant speed v in circular orbit around...
Text Solution
|
- Two bodies, each of mass M, are kept fixed with a separation 2L. A par...
Text Solution
|