A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
HEATING EFFECT OF CURRENT
CENGAGE PHYSICS ENGLISH|Exercise Integer|5 VideosHEATING EFFECT OF CURRENT
CENGAGE PHYSICS ENGLISH|Exercise Calculating Thermal Power in Resistance|14 VideosHEATING EFFECT OF CURRENT
CENGAGE PHYSICS ENGLISH|Exercise Assertion - Reasoning|6 VideosGEOMETRICAL OPTICS
CENGAGE PHYSICS ENGLISH|Exercise Integer Type|4 VideosINDUCTANCE
CENGAGE PHYSICS ENGLISH|Exercise Concept Based|8 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-HEATING EFFECT OF CURRENT-Comprehension
- In figure circuit section AB absorbs energy at the rate of 5.0 W when ...
Text Solution
|
- In figure circuit section AB absorbs energy at the rate of 5.0 W when ...
Text Solution
|
- A three - way light bulb has three brightness settings ( low , medium ...
Text Solution
|
- A three - way light bulb has three brightness settings ( low , medium ...
Text Solution
|
- In Fig. 7.48, each of the segments ( e.g., AE , GM, etc.) has resistan...
Text Solution
|
- In Fig. 7.48, each of the segments ( e.g., AE , GM, etc.) has resistan...
Text Solution
|
- In Fig. 7.48, each of the segments ( e.g., AE , GM, etc.) has resistan...
Text Solution
|
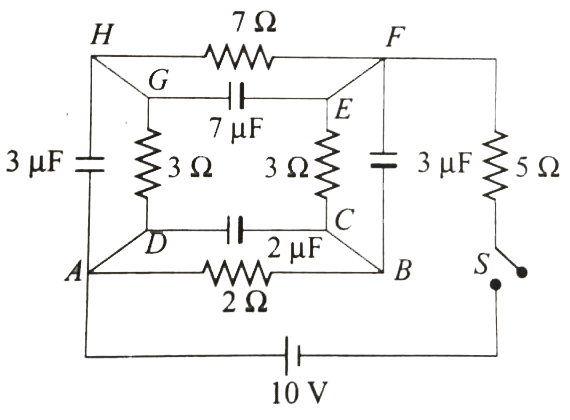
- Refer to Fig. 7.49. At t = 0 , the switch is closed . Just after ...
Text Solution
|
- Refer to Fig. 7.49. Long time after closing the switch , find the...
Text Solution
|
- Refer to Fig. 7.49. Long time after closing the switch , find the...
Text Solution
|
- All bulbs consume same power. The resistance of bulb 1 is 36 Omega ...
Text Solution
|
- All bulbs consume same power. The resistance of bulb 1 is 36 Omega ...
Text Solution
|
- All bulbs consume same power. The resistance of bulb 1 is 36 Omega ...
Text Solution
|