Home
Class 12
PHYSICS
If in previous illustration, The charge ...

If in previous illustration, The charge particle is projected at angle `alpha` with x-axis with magnitude of velocity. Find
a. velocity vector in function of time `vec v (t).`
b. position vector in function of time `vec r (t).`

Text Solution

Verified by Experts

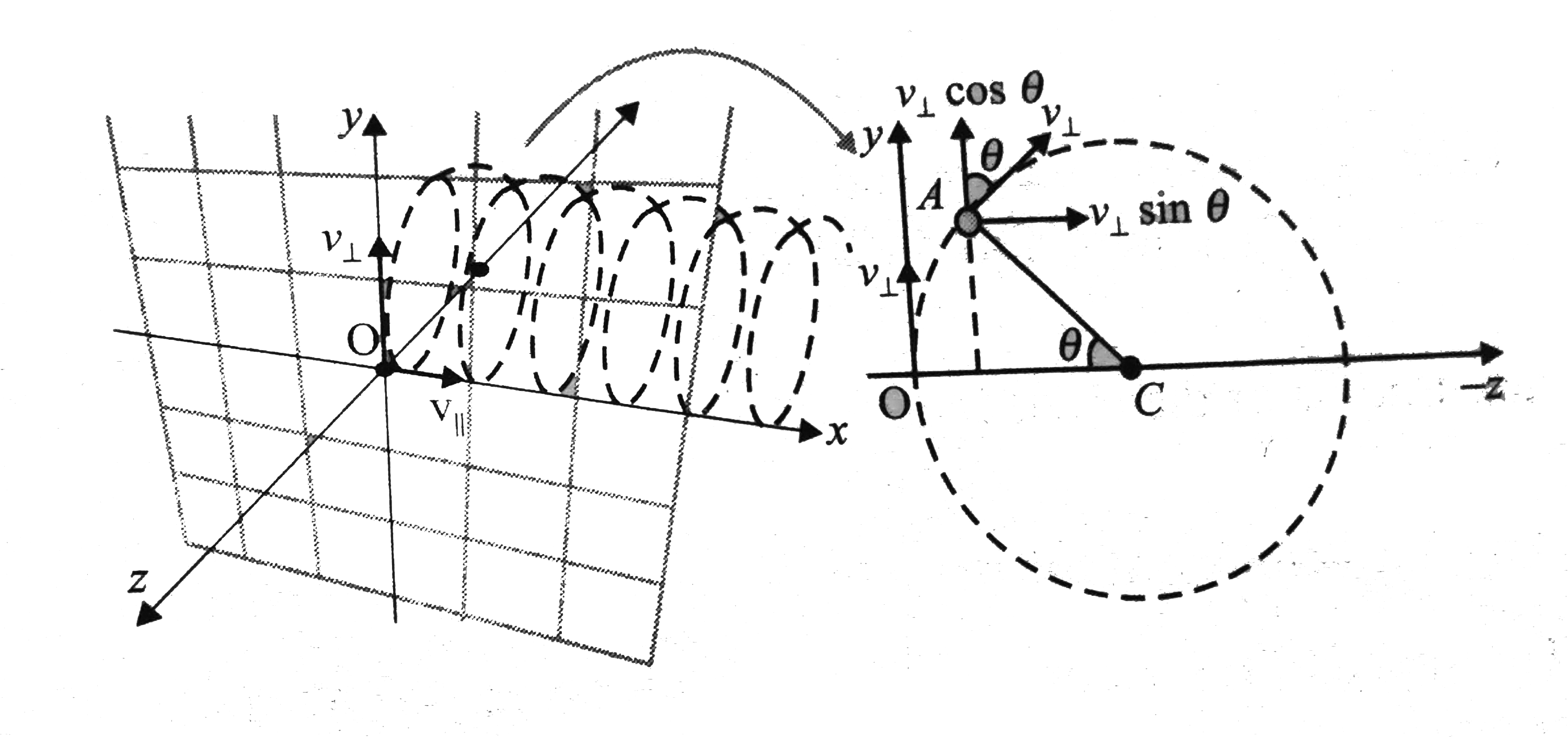
We can make components of the velocity of the particle along x-axis and y-axis. The component which is along the magnetic field will remain unchanged. But the component perpendicular to the magnetic field will provide circular motion. In a combined way, the path of the particle will be helical.

The component of velocity parallel to magnetic field
`v_(||)=v cos alpha`
The component of velocity perpendicular to magnetic field
`v_(bot)=v sin alpha`
The y and z components of velocity and position vector can be calculated in the same way as in previous illustration. The only difference is in place of v we substitute `v_(bot)`. Hence, velocity vector `[vecv_(bot)(t)]` in function of time can be writtens as
`vecv_(bot)(t)=v_(bot)cos. (qB)/m t hatj-v_(bot) sin. (qB)/m t hatk`
Hence net velocity
`vec (v) =v_(||)hat(i)+v_(bot) cos.(qB)/(m)t hat(j)-v_(bot) sin.(qB)/(m)t hat(k)`
And position vector in function of time
`vecr(t)=v_(||)t hati+R sin.(qBt)/m hatj-R(1-cos.(qBt)/m)hatk`.
Promotional Banner

Topper's Solved these Questions

  • MAGNETIC FIELD AND MAGNETIC FORCES

    CENGAGE PHYSICS ENGLISH|Exercise Solved Example|25 Videos

  • MAGNETIC FIELD AND MAGNETIC FORCES

    CENGAGE PHYSICS ENGLISH|Exercise Exercise 1.1|22 Videos

  • INDUCTANCE

    CENGAGE PHYSICS ENGLISH|Exercise Concept Based|8 Videos

  • MISCELLANEOUS VOLUME 3

    CENGAGE PHYSICS ENGLISH|Exercise True and False|3 Videos

Similar Questions

Explore conceptually related problems

A charge particle of mass m and charge q is projected with velocity v along y-axis at t=0. Find the velocity vector and position vector of the particle vec v (t) and vec r (t) in relation with time.

A particle is projected with velocity u at angle theta with horizontal. Find the time when velocity vector is perpendicular to initial velocity vector.

A particle is projected with velocity u at angle theta with horizontal. Find the time when velocity vector is perpendicular to initial velocity vector.

A projectile is projected at an angle alpha with an initial velocity u. The time t, at which its horizontal velocity will equal the vertical velocity for the first time

Acceleration of particle moving along the x-axis varies according to the law a=-2v , where a is in m//s^(2) and v is in m//s . At the instant t=0 , the particle passes the origin with a velocity of 2 m//s moving in the positive x-direction. (a) Find its velocity v as function of time t. (b) Find its position x as function of time t. (c) Find its velocity v as function of its position coordinates. (d) find the maximum distance it can go away from the origin. (e) Will it reach the above-mentioned maximum distance?

A particle travels so that its acceleration is given by vec(a)=5 cos t hat(i)-3 sin t hat(j) . If the particle is located at (-3, 2) at time t=0 and is moving with a velocity given by (-3hat(i)+2hat(j)) . Find (i) The velocity [vec(v)=int vec(a).dt] at time t and (ii) The position vector [vec(r)=int vec(v).dt] of the particle at time t (t gt 0) .

The position x of a particle varies with time t according to the relation x=t^3+3t^2+2t . Find the velocity and acceleration as functions of time.

A projectill is projected at an angle (alpha gt 45^(@)) with an initial velocity u. The time t, at which its magnitude of horizontal velocity will equal the magnitude of vertical velocity is :-

A particle is projected from ground at angle 45^@ with initial velocity 20(sqrt2) m//s . Find (a) change in velocity, (b) magnitude of average velocity in a time interval from t=0 to t=3s .

A particle is projected with a speed v and an angle theta to the horizontal. After a time t, the magnitude of the instantaneous velocity is equal to the magnitude of the average velocity from 0 to t. Find t.