Home
Class 12
PHYSICS
A conductor (rod) of mass m, length l ca...

A conductor (rod) of mass m, length `l` carrying a current i is subjected to a magnetic field of induction B. If the coefficients of friction between the conducting rod and rail is `mu,` find the value of I if the rod starts sliding.

Text Solution

Verified by Experts

The magnetic force is `F_m=ilB sinvarphi`,
where `varphi_B` =Angle between current and magnetic field =`90^@`.
or `F_m=ilB`
but it acts at an angle `theta` with horizontal as shown in Fig. according to Fleming's left hand rule.
Then the net force along x- and y-axis are
`F_y=N-(mg+F_m sin theta)=0`
or `N=mg+F_msin theta`....(i)
`F_x=f-F_m cos theta=0`....(ii)
or `f=F_m cos theta`
Law of friction, `f=muN`....(iii)
By using the above equations
`mu(mg+F_msin theta)=F_m cos theta`
or `F_m=(mumg)/(cos theta-musin theta) or ilB=(mumg)/(cos theta-musin theta)`
or `i=(mumg)/(lB(cos theta-musin theta))`
.
Promotional Banner

Topper's Solved these Questions

  • MAGNETIC FIELD AND MAGNETIC FORCES

    CENGAGE PHYSICS ENGLISH|Exercise Solved Example|25 Videos

  • MAGNETIC FIELD AND MAGNETIC FORCES

    CENGAGE PHYSICS ENGLISH|Exercise Exercise 1.1|22 Videos

  • INDUCTANCE

    CENGAGE PHYSICS ENGLISH|Exercise Concept Based|8 Videos

  • MISCELLANEOUS VOLUME 3

    CENGAGE PHYSICS ENGLISH|Exercise True and False|3 Videos

Similar Questions

Explore conceptually related problems

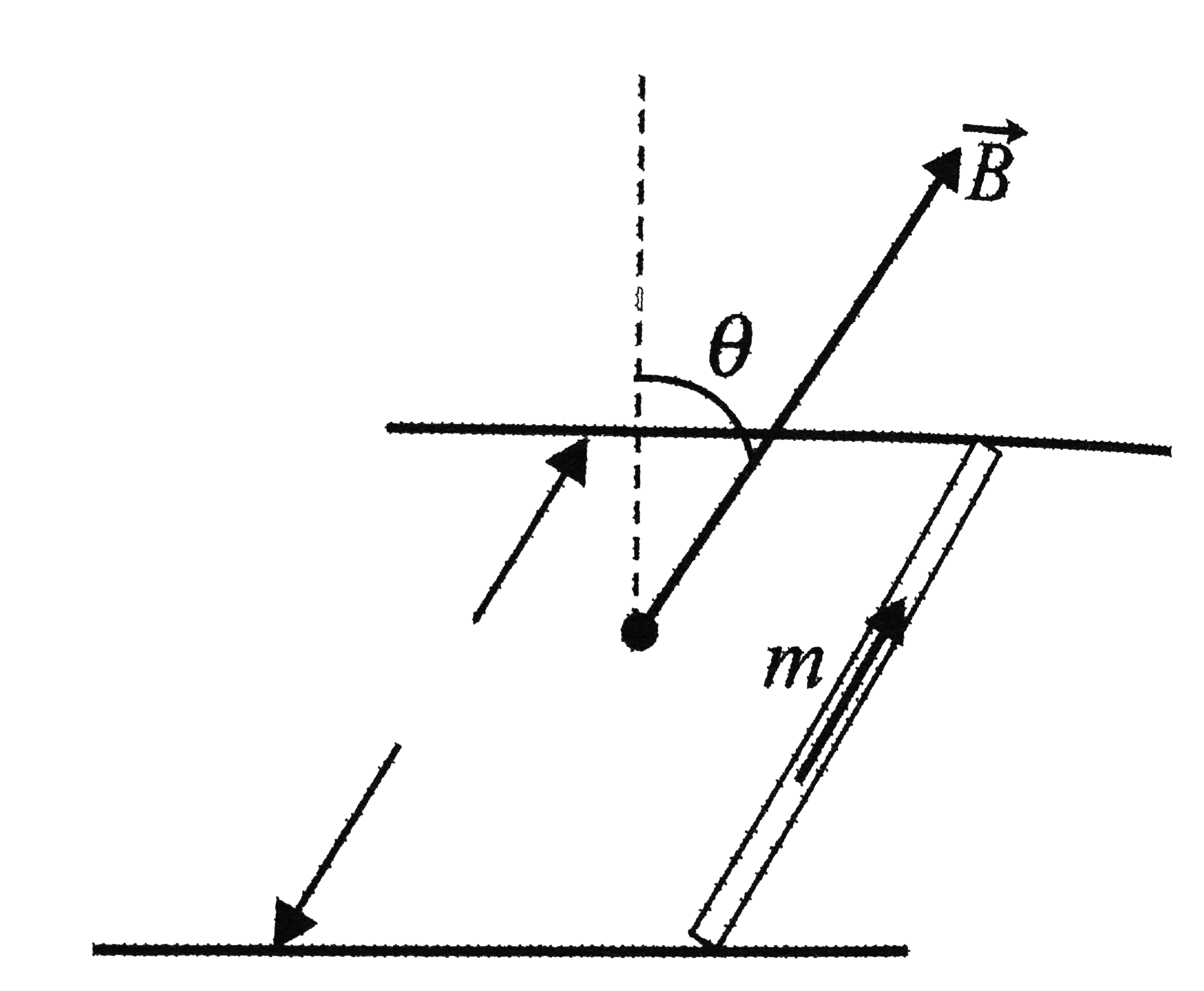
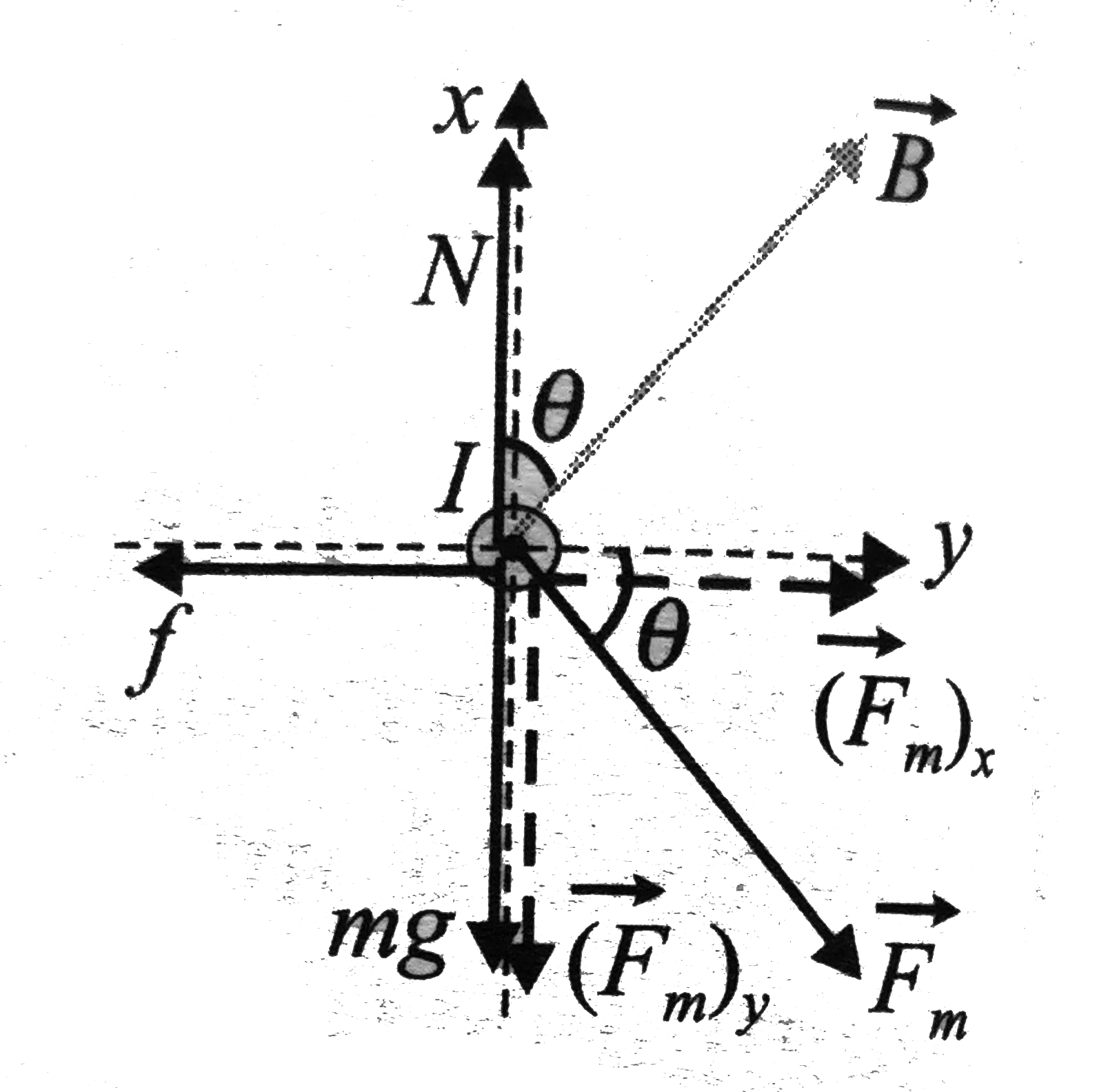On an inclined plane, two conducting rails are fixed along the line of greatest slope. A conducting rod AB is placed on the radils so that it is horizontal. A vertically upward uniform magnetic field is present in the region. A current i flows through AB from B to A. The mass of AB is m and the coefficient of friction between the rod and rails is mu . Find the minimum and maximum value of B, so that the rod can stay in equilibrium. Assume that mu lt tan theta

A square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is (dependence on L)

A conducting rod of length 'l'=2sqrt(5) meter and mass 'm'=4kg lies on the horizontal table. Coefficient of friction between the rod and the table is 'mu'=(1/2) . If the current in the conductor si 2 ampere, then find the minimum magnitude of magnetic field strength (in Tesla) such that conducting rod just starts to translate along x -axis (take g=10m//sec^(2) ) [neglect the radius of rod]

A rod CD of length b carrying a current l, is placed in a magnetic field due to a thin log wire AB carrying currrent I as shown in fig. Then find the net force experienced by the wire

A copper rod of mass m rests on two horizontal rails distance L apart and carries a current of I from one rail to the other. The coefficient of static friction between rod and rails is mu_(s) What are the (a) magnitude and (b) angle (relative to the vertical) of the smallest magnetic field that puts the rod on the verge of sliding?

A conducting rod of length l is moving in a transverse magnetic field of strength B with veocity v. The resistance of the rod is R. The current in the rod is

A straight wire of length l can slide on two parallel plastic rails kept in a horizontal plane with a separation d. The coefficient of friction between the wire and the rails is mu . If the wire carries a current I, what minimum magnetic field should exist in the space in order to slide the wire on the rails.

A loop is formed by two parallel conductors connected by a solenoid with inductance L=2H and a conducting rod of mass m=80g, which can freely (without fricition) slide over the conductors. The conductors are located in a horizontal plane in a uniform vertical magnetic field with induction B=4T. The distance between the conductors is equal to l=4cm. At the moment t=0 the rod is imparted an initial velocity v_(0)=2 cm//s directed to the right. Find the amplitude (in cm) for the oscillations of conducting rod, if the electric resistance of the loop is negligible.

A small conducting rod of length l, moves with a uniform velocity v in a uniform magnetic field B as shown in fig __

A copper rod of length L rotates with an angular with an angular speed 'omega' in a uniform magnetic field B. find the emf developed between the two ends of the rod. The field in perpendicular to the motion of the rod.