Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
ELECTROMAGNETIC INDUCTION
CENGAGE PHYSICS ENGLISH|Exercise Exercises Single Correct|79 VideosELECTROMAGNETIC INDUCTION
CENGAGE PHYSICS ENGLISH|Exercise Exercises Multiple Correct|23 VideosELECTROMAGNETIC INDUCTION
CENGAGE PHYSICS ENGLISH|Exercise Exercise 3.2|27 VideosELECTRICAL MEASURING INSTRUMENTS
CENGAGE PHYSICS ENGLISH|Exercise M.C.Q|2 VideosELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYS
CENGAGE PHYSICS ENGLISH|Exercise dpp 3.3|15 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-ELECTROMAGNETIC INDUCTION-Exercises Subjective
- A long thin wire carrying a varying current I = i(0) sin omegat lies a...
Text Solution
|
- A wire is bent into three circular segment of radius r = 10 cm as sho...
Text Solution
|
- Three identical wires are bent into semi-circular arcs to each of radi...
Text Solution
|
- Electric circuit is composed of three conducting rods MO, ON and PQ as...
Text Solution
|
- The wire loop, shown in , is made by taking a flat rectangular loop of...
Text Solution
|
- A rod of mass m can rotate without friction about axis sliding (also w...
Text Solution
|
- A square shaped, conducting wire loop of side L, total mass m and tota...
Text Solution
|
- CDEF is a fixed conducting smooth frame in vertical plane. A conductin...
Text Solution
|
- The entire network shown here, has uniform wire having resistance per ...
Text Solution
|
- Two fixed long straight wires carry the same current i in opposite dir...
Text Solution
|
- Two parallel, long, straight conductor lie on a smooth plane surface. ...
Text Solution
|
- The rectangualr wire- frame, shown in has a width d, mass m, resist...
Text Solution
|
- , ABCEFGA is a square conducting frame of side 2 m and resistance 1 Om...
Text Solution
|

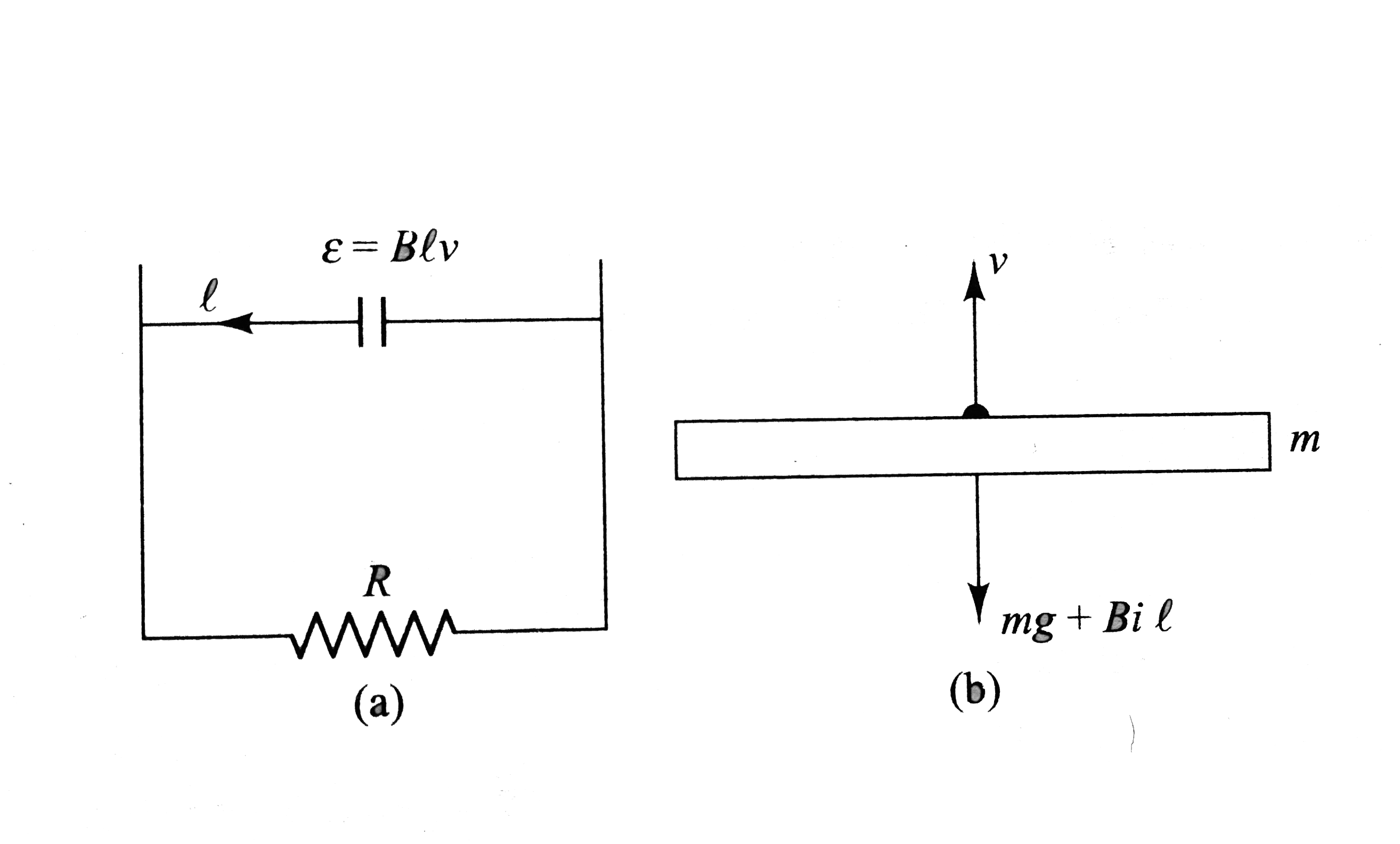 ,
, 