Text Solution
Verified by Experts
Topper's Solved these Questions
INDUCTANCE
CENGAGE PHYSICS ENGLISH|Exercise Solved Examples|3 VideosINDUCTANCE
CENGAGE PHYSICS ENGLISH|Exercise Exercise 4.1|24 VideosHEATING EFFECT OF CURRENT
CENGAGE PHYSICS ENGLISH|Exercise Thermal Power in Resistance Connected in Circuit|27 VideosMAGNETIC FIELD AND MAGNETIC FORCES
CENGAGE PHYSICS ENGLISH|Exercise Multiple Correct Answer type|2 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-INDUCTANCE-Concept Based
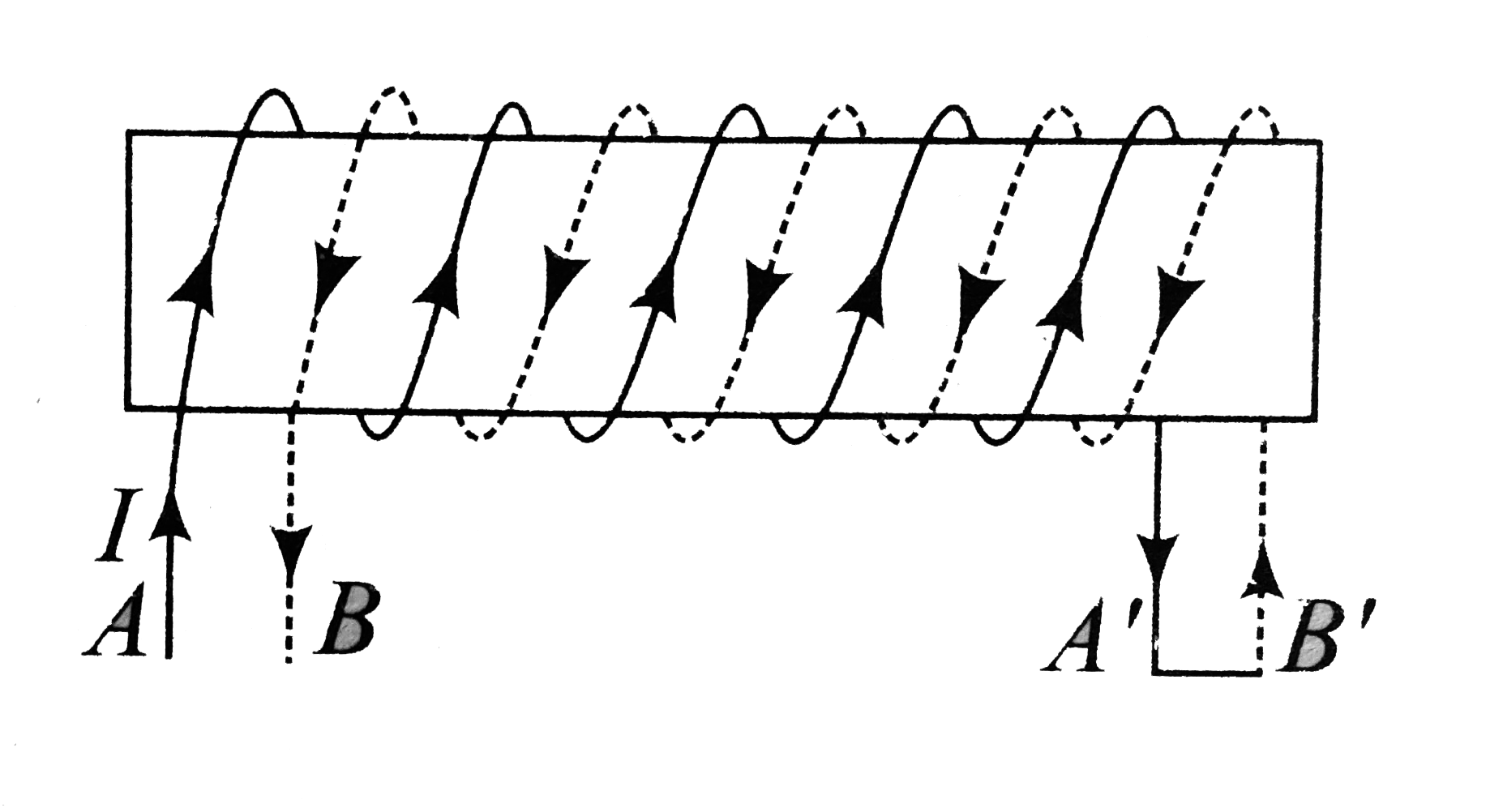
- In Fig. coil 1 and coil 2 are wound on a long cylindrical insulator. T...
Text Solution
|
- Light is incident on a glass plate of refractive index 3.0 such that a...
Text Solution
|
- After switch is closed in the LC circuit shown in the figure, the char...
Text Solution
|
- Discuss the similarities between the energy stored in the electric fie...
Text Solution
|
- In the circuit of figure, the battery emf is epsi the resitance is R a...
Text Solution
|
- A 1.00 muF capacitor is charged by a 40.0 V power supply. The fully ch...
Text Solution
|
- The frequency of oscillation of current in the indcutor is
Text Solution
|
- Light of wavelength 24000A is incident on a thin glass plate of refrac...
Text Solution
|
- Two waves of intensity I and 9I are superimposed in such a way that re...
Text Solution
|