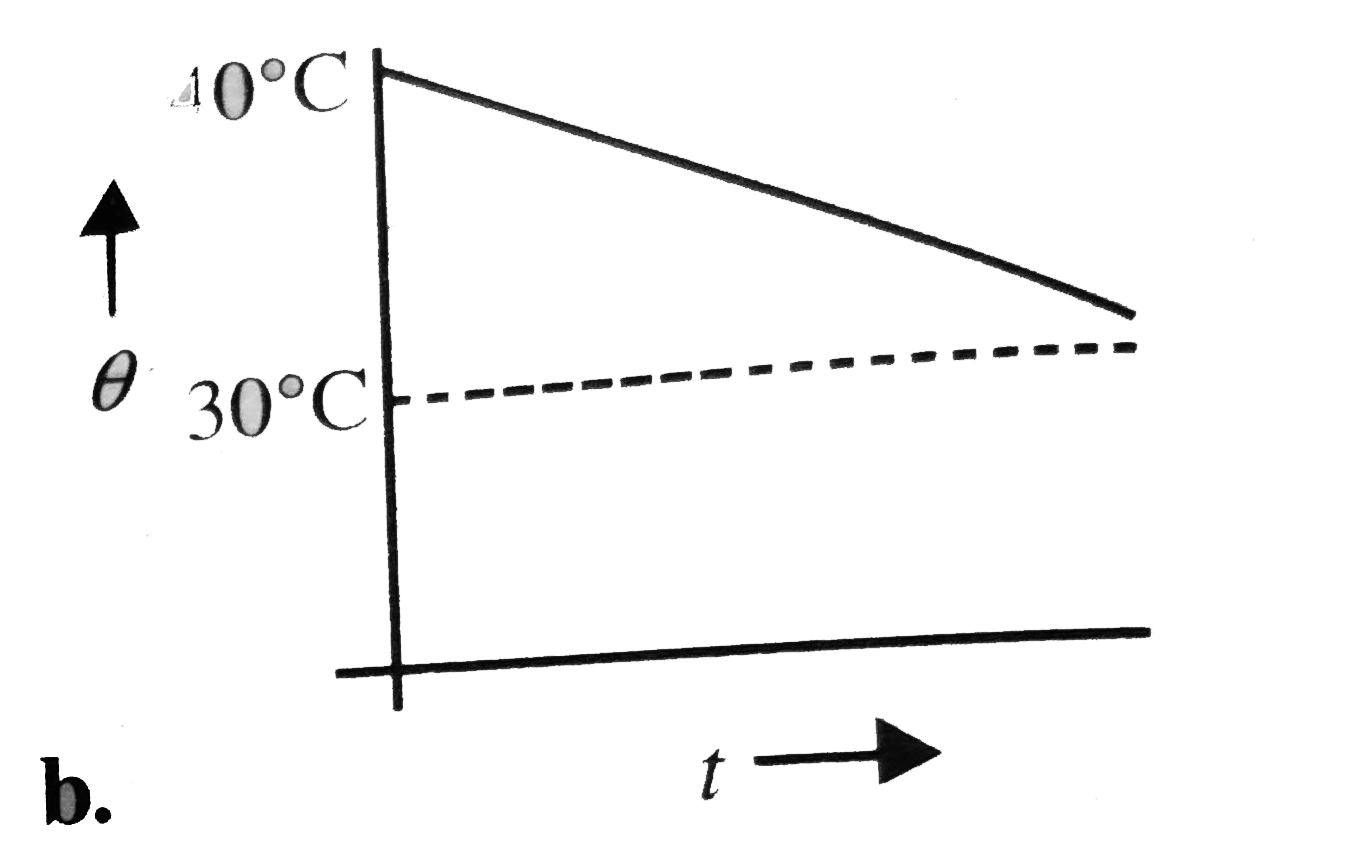
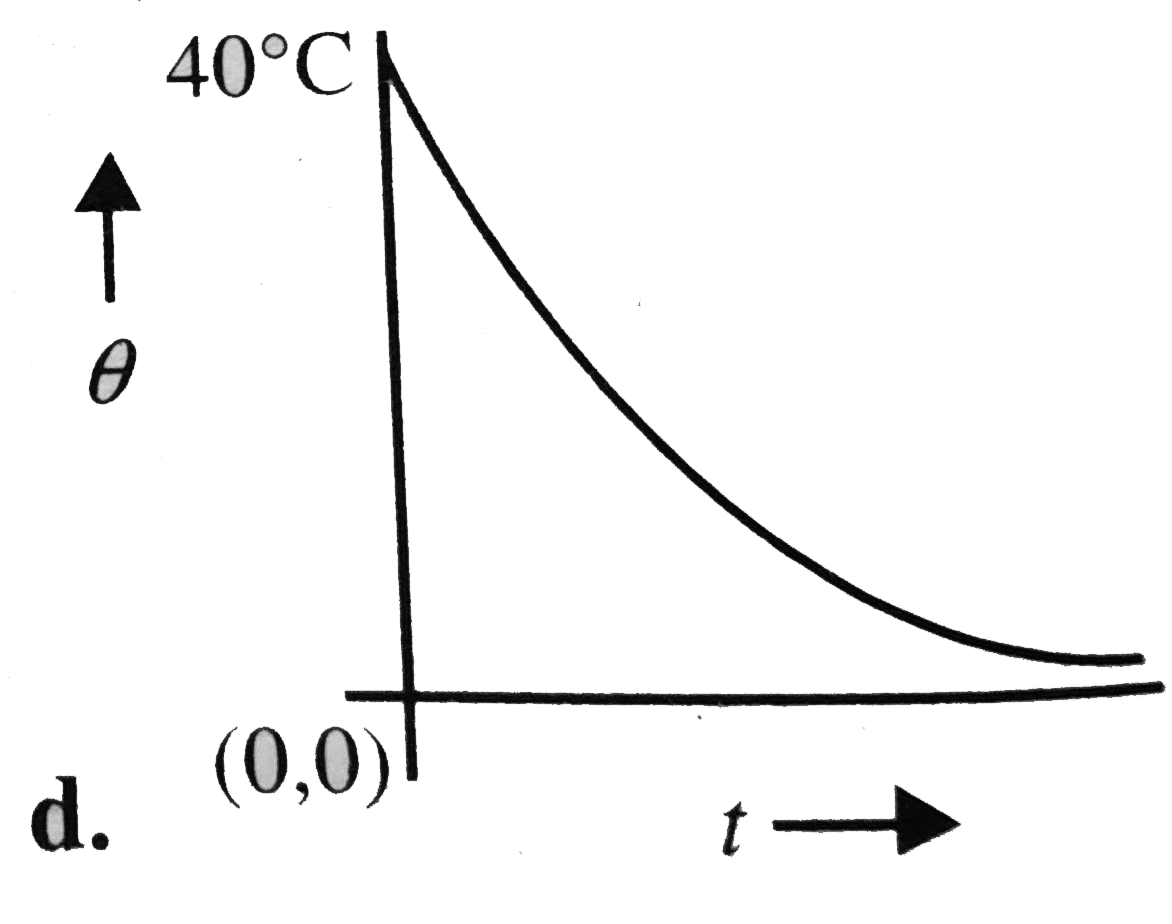
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
CALORIMETRY
CENGAGE PHYSICS ENGLISH|Exercise Integer|8 VideosCALORIMETRY
CENGAGE PHYSICS ENGLISH|Exercise Solved Example|13 VideosCALORIMETRY
CENGAGE PHYSICS ENGLISH|Exercise Multiple Correct|25 VideosBASIC MATHEMATICS
CENGAGE PHYSICS ENGLISH|Exercise Exercise 2.6|20 VideosCENTRE OF MASS
CENGAGE PHYSICS ENGLISH|Exercise INTEGER_TYPE|1 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-CALORIMETRY-Comprehension
- A body cools in a surrounding of constant temperature 30^@C Its heat c...
Text Solution
|
- A body cools in a surrounding of constant temperature 30^@C Its heat c...
Text Solution
|
- A body cools in a surrounding of constant temperature 30^@C Its heat c...
Text Solution
|
- The internal energy of a solid also increases when heat is transferred...
Text Solution
|
- The internal energy of a solid also increases when heat is transferred...
Text Solution
|
- The internal energy of a solid also increases when heat is transferred...
Text Solution
|
- A wire of length 1 m and radius 10^-3m is carrying a heavy current and...
Text Solution
|
- A wire of length 1 m and radius 10^-3m is carrying a heavy current and...
Text Solution
|
- A wire of length 1 m and radius 10^-3m is carrying a heavy current and...
Text Solution
|
- Assume that the thermal conductivity of copper is twice that of alumin...
Text Solution
|
- Assume that the thermal conductivity of copper is twice that of alumin...
Text Solution
|
- Assume that the thermal conductivity of copper is twice that of alumin...
Text Solution
|
- A thin copper rod of uniform cross section A square metres and of leng...
Text Solution
|
- A thin copper rod of uniform cross section A square metres and of leng...
Text Solution
|
- A thin copper rod of uniform cross section A square metres and of leng...
Text Solution
|
- An immersion heater, in an insulated vessel of negligible heat capacit...
Text Solution
|
- An immersion heater, in an insulated vessel of negligible heat capacit...
Text Solution
|
- An immersion heater, in an insulated vessel of negligible heat capacit...
Text Solution
|
- A body of area 0.8xx10^-2m^2 and mass 5xx10^-4kg directly faces the su...
Text Solution
|
- A body of area 0.8xx10^(-2) m^(2) and mass 5xx10^(-4) kg directly face...
Text Solution
|