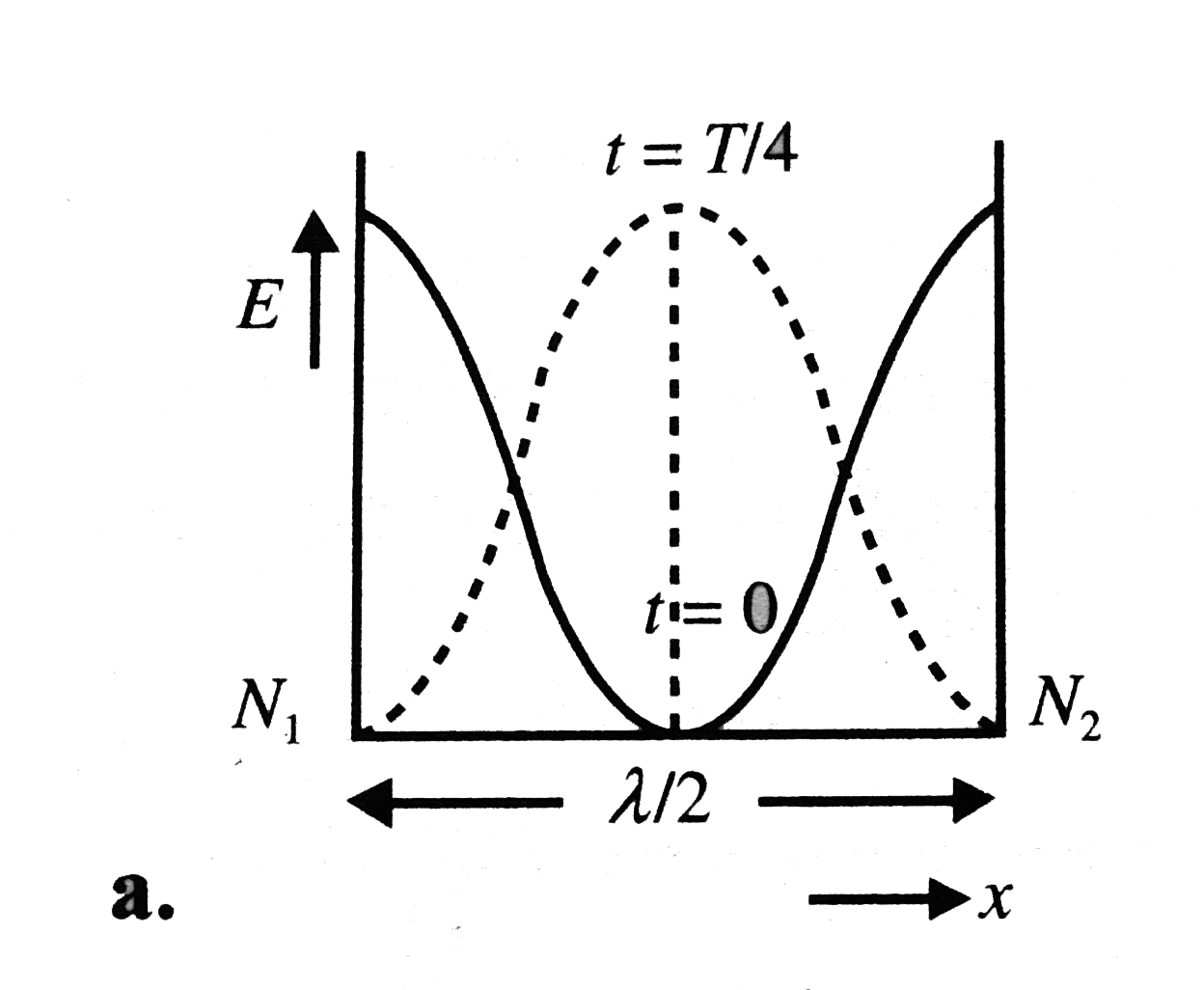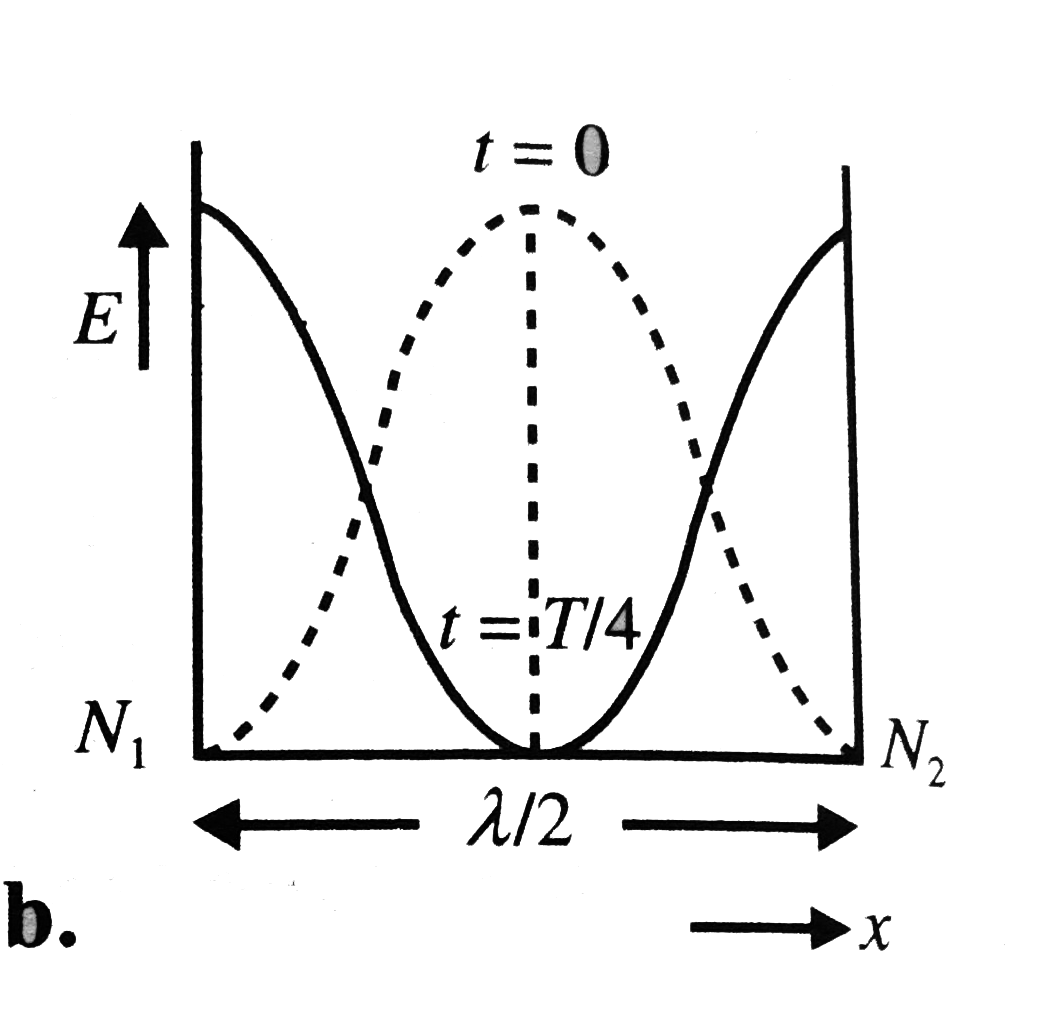A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
SUPERPOSITION AND STANDING WAVES
CENGAGE PHYSICS ENGLISH|Exercise Integer|9 VideosSUPERPOSITION AND STANDING WAVES
CENGAGE PHYSICS ENGLISH|Exercise Single Correct Answer Type|56 VideosSUPERPOSITION AND STANDING WAVES
CENGAGE PHYSICS ENGLISH|Exercise Assertion - Reasoning|6 VideosSOUND WAVES AND DOPPLER EFFECT
CENGAGE PHYSICS ENGLISH|Exercise Integer|16 VideosTHERMODYNAMICS
CENGAGE PHYSICS ENGLISH|Exercise 24|1 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-SUPERPOSITION AND STANDING WAVES-Comprehension
- A longitudinal standing wave y = a cos kx cos omega t is maintained i...
Text Solution
|
- A longitudinal standing wave y = a cos kx cos omega t is maintained i...
Text Solution
|
- A longitudinal standing wave y = a cos kx cos omega t is maintained i...
Text Solution
|
- In a standing wave experiment , a 1.2 - kg horizontal rope is fixed in...
Text Solution
|
- In a standing wave experiment , a 1.2 - kg horizontal rope is fixed in...
Text Solution
|
- In a standing wave experiment , a 1.2 - kg horizontal rope is fixed in...
Text Solution
|
- In an organ pipe (may be closed or open ) of 99 cm length standing wav...
Text Solution
|
- In an organ pipe ( may be closed or open of 99 cm length standing wave...
Text Solution
|
- In an organ pipe (may be closed or open ) of 99 cm length standing wav...
Text Solution
|
- Estimate the fraction of molecular volume to the actual volume occupie...
Text Solution
|
- Two plane harmonic sound waves are expressed by the equations. y(1)(...
Text Solution
|
- Two waves y(1) = A cos (0.5 pi x - 100 pi t) and y(2) = A cos (0.46 pi...
Text Solution
|
- Two waves y(1) = A cos (0.5 pi x - 100 pi t) and y(2) = A cos (0.46 pi...
Text Solution
|
- An oscillator of frequency 680 Hz drives two speakers . The speakers a...
Text Solution
|
- An oscillator of frequency 680 Hz drives two speakers . The speakers a...
Text Solution
|
- An oscillator of frequency 680 Hz drives two speakers . The speakers a...
Text Solution
|
- An oscillator of frequency 680 Hz drives two speakers . The speakers a...
Text Solution
|
- Consider a standing wave formed on a string . It results due to the su...
Text Solution
|
- Consider a standing wave formed on a string . It results due to the su...
Text Solution
|
- Consider a standing wave formed on a string . It results due to the su...
Text Solution
|