Home
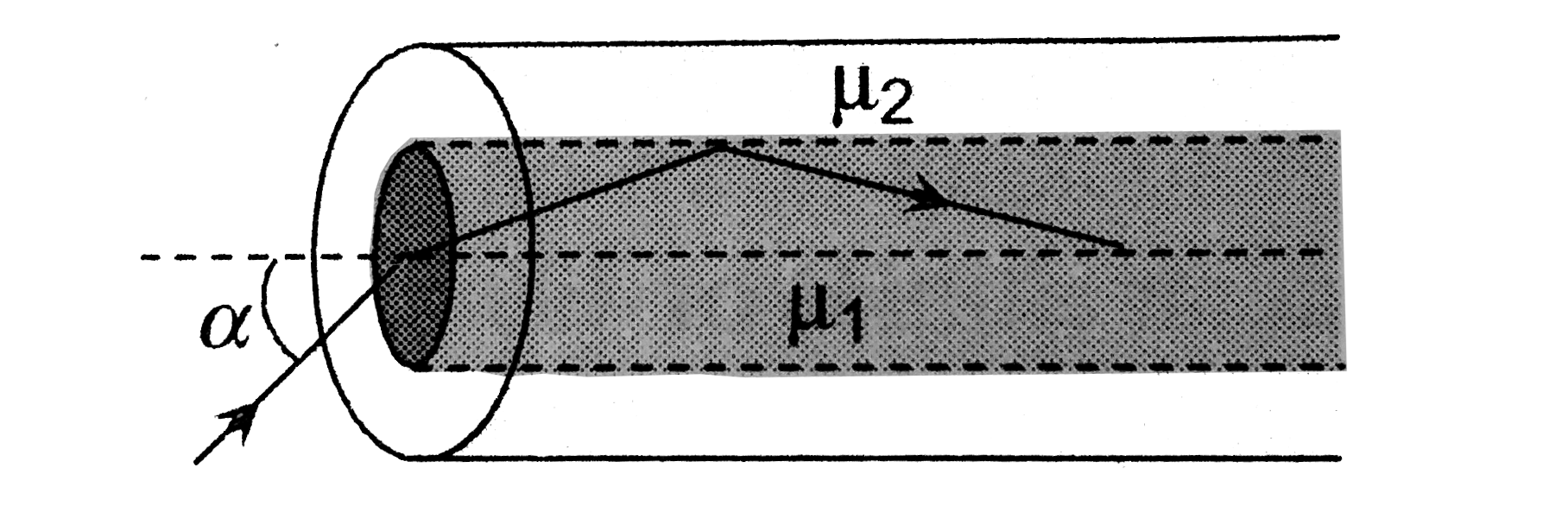
Class 12
PHYSICS
An optical fibre consists of core of mu(...

An optical fibre consists of core of `mu_(1)` surrounded by a cladding of `mu_(2) lt mu_(1)`. A beam of light enters from air at an angle `alpha` with axis of fibre. The highest `alpha` for which ray can be travelled through fibre is

A

`cos^(-1) sqrt(mu_(2)^(2)-mu_(1)^(2))`

B

`sin^(-1)sqrt(mu_(1)^(2)-mu_(2)^(2))`

C

`tan^(-1) sqrt(mu_(1)^(2)-mu_(2)^(2))`

D

`sec^(-1) sqrt(mu_(1)^(2)-mu_(2)^(2))`

Text Solution

Verified by Experts

The correct Answer is:
B
Promotional Banner

Topper's Solved these Questions

  • RAY OPTICS

    CENGAGE PHYSICS ENGLISH|Exercise DPP 1.3|14 Videos

  • RAY OPTICS

    CENGAGE PHYSICS ENGLISH|Exercise DPP 1.4|15 Videos

  • RAY OPTICS

    CENGAGE PHYSICS ENGLISH|Exercise Matching Column Type|1 Videos

  • PHOTOELECTRIC EFFECT

    CENGAGE PHYSICS ENGLISH|Exercise Integer Type|4 Videos

  • SOURCES OF MAGNETIC FIELD

    CENGAGE PHYSICS ENGLISH|Exercise single correct Ansewer type|12 Videos

Similar Questions

Explore conceptually related problems

An optical fibre having core of refractive index sqrt3 and cladding of refractive index 1.5 is kept in air. The maximum angle of acceptance is

The optical fibres have in an inner core of refractive index n1 and a cladding of refractive index n2 such that

A cylinderical optical fibre (quarter circular shape) of refractive index n = 2 and diameter d = 4mm is surrounded by air. A light beam is sent into the fibre along its axis as shown in figure. Then the smallest outer radius R (as shown in figure) for which no light escapes after incident on curved surface of fibre is: .

There are two blocks of masses m_(1) and m_(2) , m_(1) is placed on m_(2) on a table which is rotating with an angular velocity omega about the vertical axis . The coefficent of friction between the block is mu_(1) and between m_(2) and table is mu_(2) (mu_(1) lt mu_(2)) if block are placed at distance R from the axis of ratation , for relative sliding between the surface in contact , find the a. friction force at the contacting surface b. maximum angular speed omega

A system of coordinatees is drawn in a medium whose refractive index vaires as mu=(2)/(1+Y^(2)) where 0 le y le 1 . A ray of light is incident at origin at an angle 60^(@) with y-axis as shown in figure. At point P, the ray becomes parallel to x-axis, the volue of H is -

A right angled prism of refractive index mu_(1) is placed in a rectangular block of refractive index mu_(2) , which is surrounded by a medium of refractive index mu_(3) ,as shown in the figure . A ray of light 'e' enters the rectangular block at normal incidence . depending upon the relationship between mu_(1) , mu_(2) "and" mu_(3) , it takes one of the four possible paths 'ef' , 'eg' , 'eh' or 'ef' Match the paths in List I with conditions of refractive indices in List II and select the correct answer using the codes given below the lists: {:("List" I , "List" II) , ( P. e rarr f , 1. mu_(1)gt sqrt(2mu_(2))) , ( Q. e rarr g , 2. mu_(2) gt mu_(1) "and" mu_(2) gt mu_(3)), ( R. e rarr f , 3. mu_(1) = mu_(2)), ( S. e rarr f , 4. mu_(2) lt mu_(1) lt sqrt(2mu_(2)) "and" mu_(2) gt mu_(3)):} Codes : {:( P , Q , R , S) , ((A) 2 , 3 , 1 , 4), ((B) 1 , 2 , 4 , 3) , ((C) 4 , 1 , 2 , 3) , ((D) 2, 3 , 4 , 1):}

An optical fiber has index of refraction n=1.40 and diameter d=100 mu m . It is surrounded by air. Light is sent into the fiber along the axis as shown in figure. If smallest outside radius R permitted for a bend in the fiber for no light to escape is given by 50 x ("in" mu m) fill value of x.

The refractive index of the core of an optical fibre is mu_(2) and that of the cladding is mu_(1) . The angle of incidence on the face of the core of that the light ray just under goes total internal reflection at the cladding is

If mu and mu_(2) are the refractive indices of the materials of core and cladding of an optical fibre, then loss of light due to its leakage can be minimised by having

A ray of light is refracted through a sphere whose material has a refractive index mu in such a way that it passes through the extremities of two radii which make an angle beta with each other. Prove that if alpha is the deviation of the ray caused by its passage through the sphere, then cos((beta-alpha)/2)=mu cos(beta/alpha)