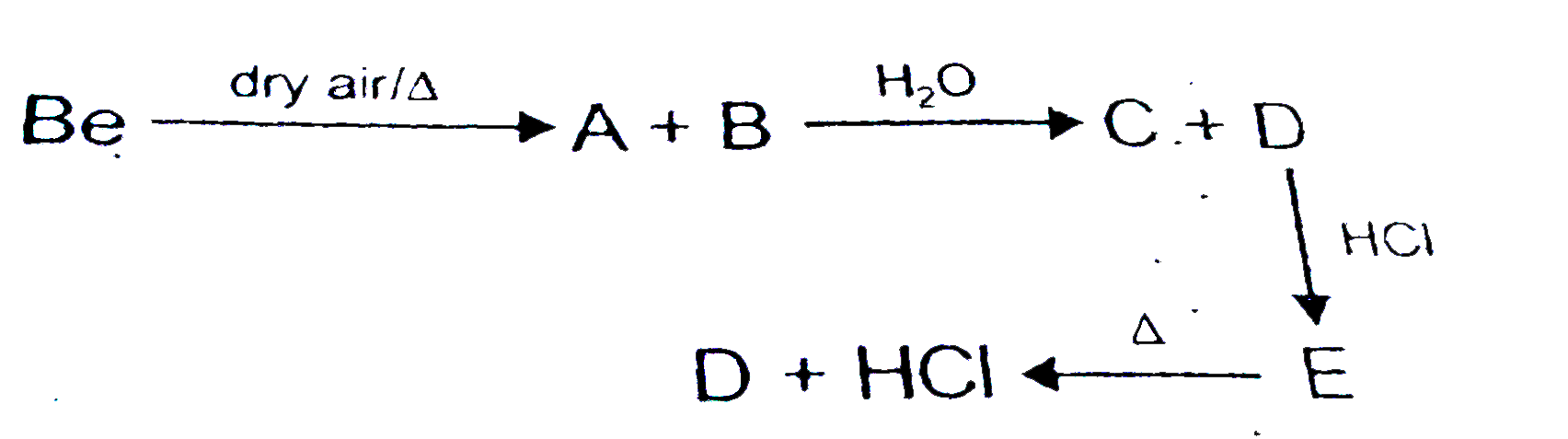A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
THE S-BLOCK ELEMENTS
AAKASH INSTITUTE ENGLISH|Exercise Assignment (Section-E)|7 VideosTHE S-BLOCK ELEMENTS
AAKASH INSTITUTE ENGLISH|Exercise Assignment (Section-F)|3 VideosTHE S-BLOCK ELEMENTS
AAKASH INSTITUTE ENGLISH|Exercise Assignment (Section-C)|11 VideosTHE P-BLOCK ELEMENTS
AAKASH INSTITUTE ENGLISH|Exercise Assignment Section-J)|16 VideosTHE SOLID STATE
AAKASH INSTITUTE ENGLISH|Exercise Assignment (SECTION - D) (ASSERTION-REASON TYPE QUESTION)|20 Videos
Similar Questions
Explore conceptually related problems
AAKASH INSTITUTE ENGLISH-THE S-BLOCK ELEMENTS-Assignment (Section-D)
- The elements of group II are known as alkaline earth metals. The elect...
Text Solution
|
- The elements of group II are known as alkaline earth metals. The elect...
Text Solution
|
- The elements of group II are known as alkaline earth metals. The elect...
Text Solution
|
- The solubility of most salts depends on the lattice energy of the soli...
Text Solution
|
- Q. Which of the following is correct order of solubility of sulphates ...
Text Solution
|
- Which of the following compounds are soluble in water?
Text Solution
|
- Q. A & B are
Text Solution
|
- Q. C & D are
Text Solution
|
- Q. C & D are
Text Solution
|