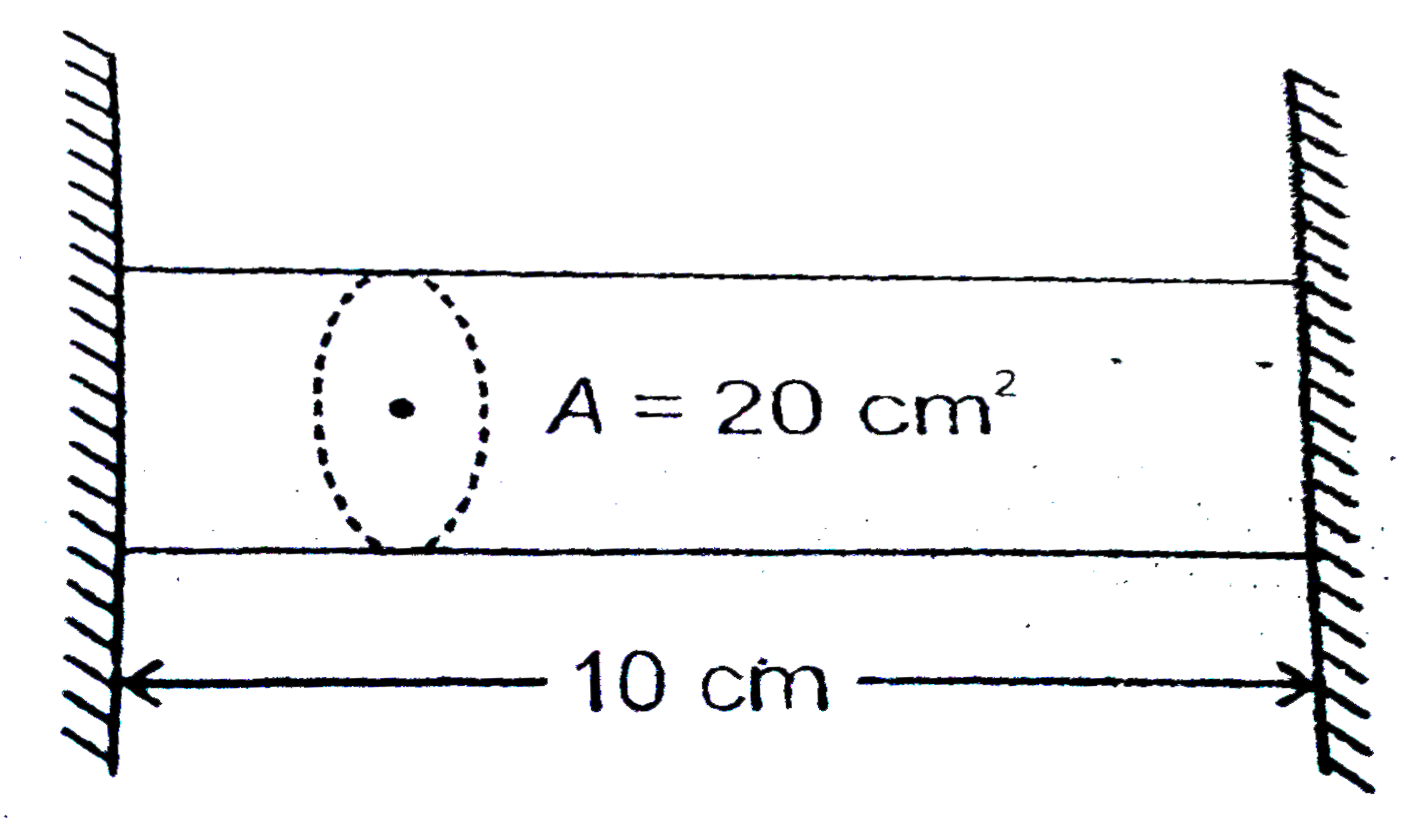Text Solution
Verified by Experts
Topper's Solved these Questions
THERMAL PROPERTIES OF MATTER
AAKASH INSTITUTE ENGLISH|Exercise Try Youself|16 VideosTHERMAL PROPERTIES OF MATTER
AAKASH INSTITUTE ENGLISH|Exercise Assignment (Section-A) Objective Type questions (one option is correct)|50 VideosTEST2
AAKASH INSTITUTE ENGLISH|Exercise EXERCISE|2 VideosTHERMODYNAMICS
AAKASH INSTITUTE ENGLISH|Exercise ASSIGNMENT (SECTION -D) (Assertion - Reason Type Questions)|10 Videos
Similar Questions
Explore conceptually related problems
AAKASH INSTITUTE ENGLISH-THERMAL PROPERTIES OF MATTER-Assignment (Section-J) Akash Challengers Questions
- An aluminum cylinder 10 cm long with a cross section area of 20cm^2 is...
Text Solution
|
- A slab of cunductivity k is in the shape of trapezoid as shown I figur...
Text Solution
|
- A cube, sphere and a cylinder made of same material shown in figure ar...
Text Solution
|
- A rod of length l with thermally insulated lateral surface consists of...
Text Solution
|
- A metallic cylindrical vessel whose inner and outer radii are r1 and r...
Text Solution
|
- A cylindrical block of length 0.4 m and area of cross-section 0.04 m^2...
Text Solution
|
- A metal ball of mass 1 kg is heated by means of a 20 W heater in a ro...
Text Solution
|
- A vessel with 100 g of water at a temperature of 0^(@)C is suspended i...
Text Solution
|