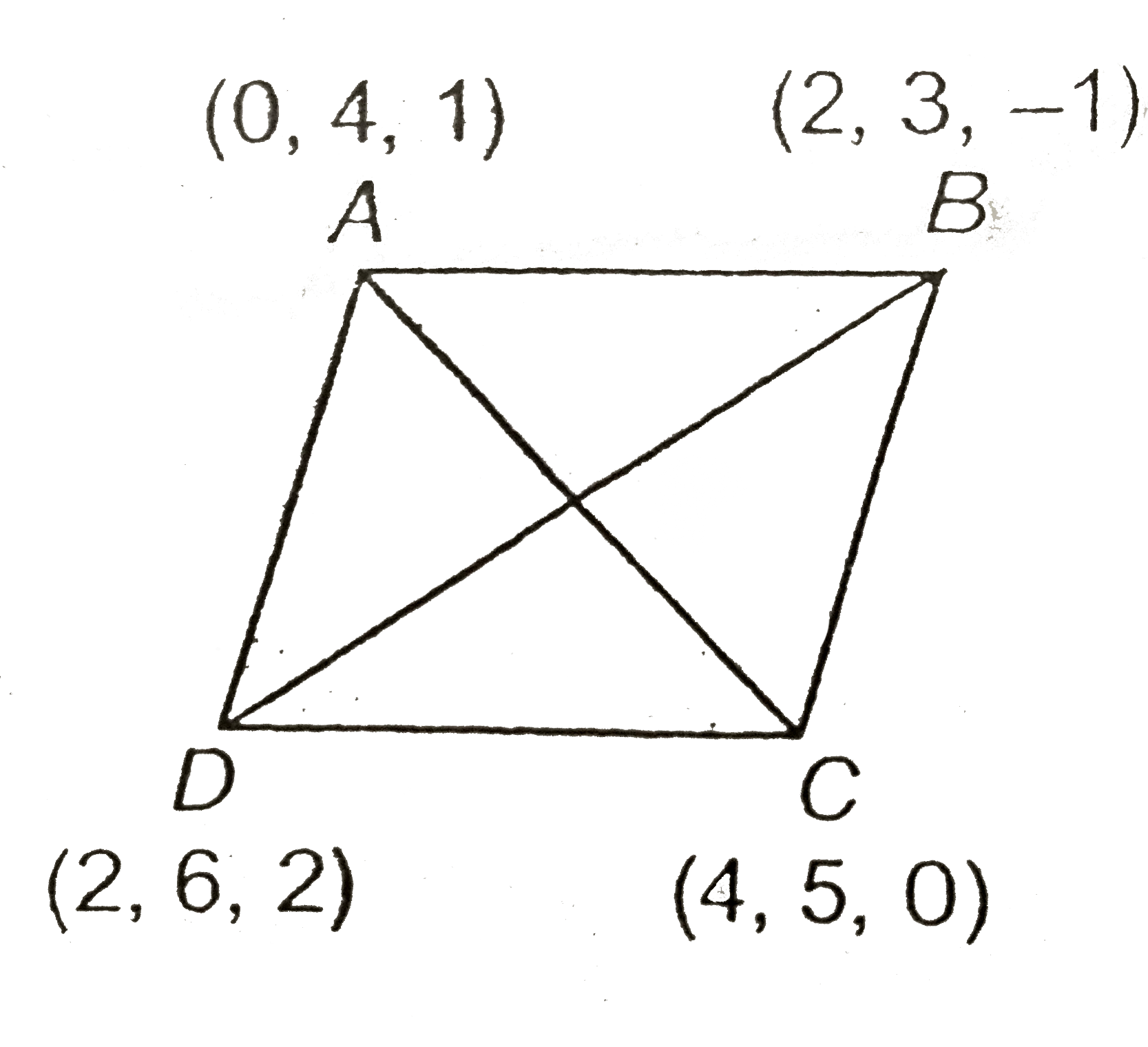Text Solution
Verified by Experts
Topper's Solved these Questions
THREE DIMENSIONAL GEOMETRY
AAKASH INSTITUTE ENGLISH|Exercise Illustration|4 VideosTHREE DIMENSIONAL GEOMETRY
AAKASH INSTITUTE ENGLISH|Exercise TRY YOURSELF|97 VideosSTRAIGHT LINES
AAKASH INSTITUTE ENGLISH|Exercise SECTION-J (AAKASH CHALLENGERS QUESTIONS)|5 VideosTRIGNOMETRIC FUNCTIONS
AAKASH INSTITUTE ENGLISH|Exercise Section - J (Akash Challengers Question)|16 Videos
Similar Questions
Explore conceptually related problems
AAKASH INSTITUTE ENGLISH-THREE DIMENSIONAL GEOMETRY -ASSIGNMENT SECTION - J
- Prove that the points A(0, 4, 1), B(2, 3, -1), C(4, 5, 0) and D(2, 6, ...
Text Solution
|
- Prove that the two lines whose direction cosines are given by the rela...
Text Solution
|
- The point in which the join of (-9, 4, 5) and (11, 0, -1) is met by t...
Text Solution
|
- Verify the following: (5,-1,1),(7,-4,7), (1,-6,10) and (-1,-3,4) are ...
Text Solution
|
- The pair of lines whose direction cosines are given by the equations 3...
Text Solution
|
- If three mutually perpendicular lines have direction cosines (l1,m1,n...
Text Solution
|
- If the plane ax+by=0 is rotated about its line of intersection with th...
Text Solution
|
- Find the equations of the projection of the line (x+1)/- 2=(y-1)/3=(z+...
Text Solution
|
- The shortest distance between a diagonal of unit cube and a diagonal ...
Text Solution
|
- Prove that the planes x - z - 1 = 0, x + y - 2z - 3 = 0 and x - 2y + z...
Text Solution
|
- The plane x- y - z = 2 is rotated through an angle pi/2 about its line...
Text Solution
|