A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
BINOMIAL THEOREM
AAKASH INSTITUTE ENGLISH|Exercise Assignment (section-B)|34 VideosBINOMIAL THEOREM
AAKASH INSTITUTE ENGLISH|Exercise Assignment (section-C) Objective type question (More than one correct answer)|15 VideosBINOMIAL THEOREM
AAKASH INSTITUTE ENGLISH|Exercise Try Yourself|20 VideosAPPLICATION OF INTEGRALS
AAKASH INSTITUTE ENGLISH|Exercise Assignment Section - I Aakash Challengers Questions|2 VideosCOMPLEX NUMBERS AND QUADRATIC EQUATIONS
AAKASH INSTITUTE ENGLISH|Exercise section-J (Aakash Challengers Qestions)|13 Videos
Similar Questions
Explore conceptually related problems
AAKASH INSTITUTE ENGLISH-BINOMIAL THEOREM-Assignment (section-A)
- The term containing a^(3)b^(4) in the expansion of (a-2b)^(7) is
Text Solution
|
- The coefficient of the term independent of x in the expansion of (x-3/...
Text Solution
|
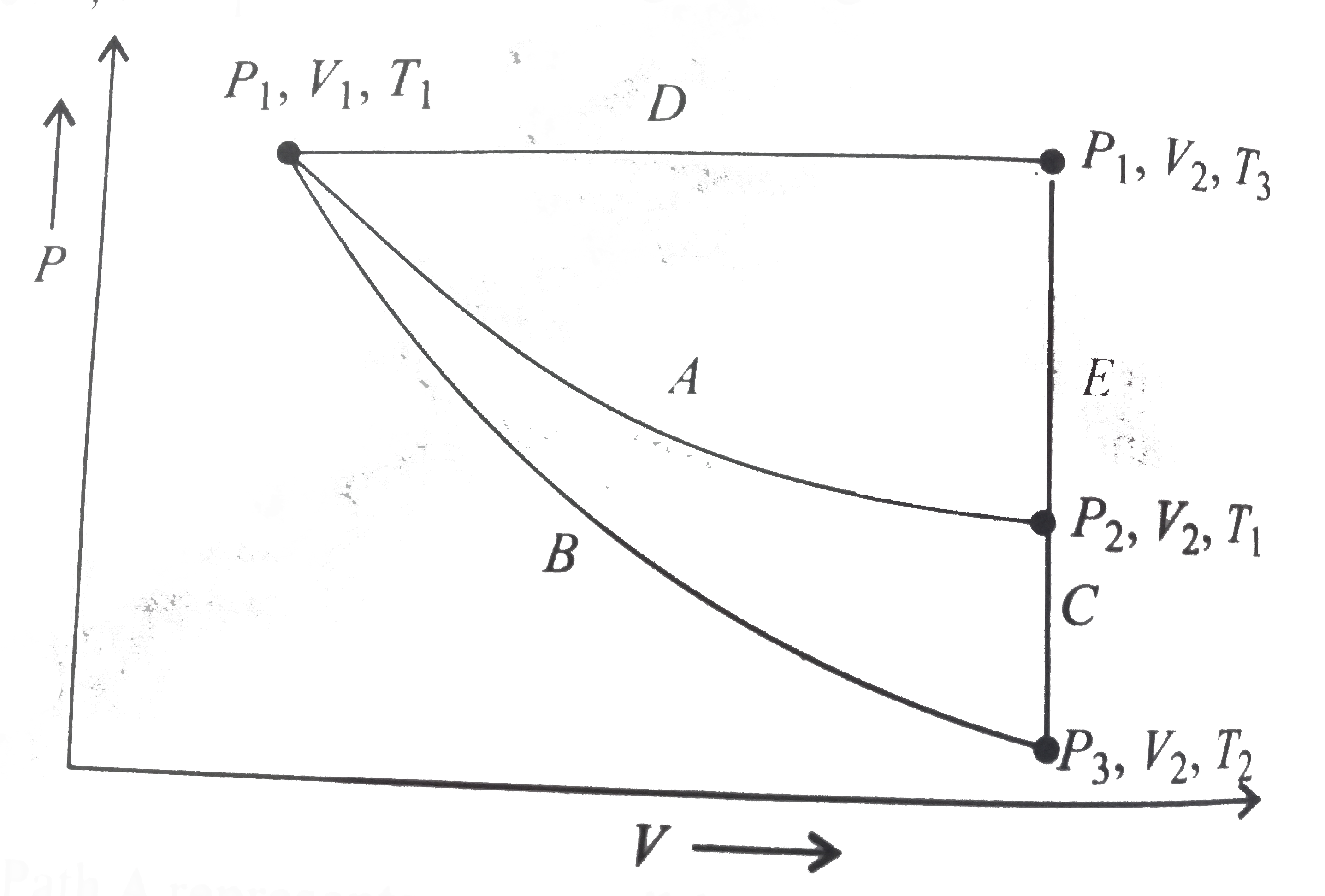
- For an ideal gas, an illustration of three different paths A,(B+C) and...
Text Solution
|
- If p a n d q are positive, then prove that the coefficients of x^pa n ...
Text Solution
|
- The number of terms in expansion of {(a+4b)^(3)(a-4b)^(3)}^(2) is
Text Solution
|
- If r^(th) term in the expansion of (x^(2)+1/x)^(12) is independent of ...
Text Solution
|
- Find the number of nonzero terms in the expansion of (1+3sqrt(2)x)^9+(...
Text Solution
|
- In the expansion of (2+1/(3x))^(n), the cofficient of x^(-7) and x^(-...
Text Solution
|
- In in the expansion of (1+px)^(q), q belongs to N, the coefficients of...
Text Solution
|
- The expansion of (x^(alpha)+1/x^(beta))^(n) has constant term, if
Text Solution
|
- The number of rational terms in the expansion of ((25)^(1/3) + 1/(25)^...
Text Solution
|
- The number of zeros at the end of (101)^(11)-1 is
Text Solution
|
- In the expantion of (1+kx)^(4) the cofficient of x^(3) is 32, then th...
Text Solution
|
- In the expansion of (3+x/2)^(n) the coefficients of x^(7) and x^(8) ar...
Text Solution
|
- sqrt(5){(sqrt(5)+1)^(50)-(sqrt(5)-1)^(50)}
Text Solution
|
- In expansion of (x+a)^(5), T(2):T(3)=1:3, then x:a is equal to
Text Solution
|
- If the coefficient of x^(7)in [ax^(2) + (1/bx)]^(11) equals the coeffi...
Text Solution
|
- The middle term in the expansioin of (1+x)^(2n) is
Text Solution
|
- Cofficient of x^(12) in the expansion of (1+x^(2))^50(x+1/x)^(-10)
Text Solution
|
- The number of terms in expansion of (x^(2)+18x+81)^(15) is
Text Solution
|