Home
Class 12
PHYSICS
Find time constant of the circuit when...

Find time constant of the circuit when (a) S is closed . (b) S is open.

Text Solution

Verified by Experts

(a) When S is closed `tau = [ R_(2) + (R_(1)R_(3))/(R_(1)+R_(3))]C `
(b) When S is open `tau = (R_(2)+R_(3))C`
Promotional Banner

Topper's Solved these Questions

  • CURRENT ELECTRICITY

    AAKASH INSTITUTE ENGLISH|Exercise Try Yourself|34 Videos

  • CURRENT ELECTRICITY

    AAKASH INSTITUTE ENGLISH|Exercise ASSIGNMENT(SECTION-A(OBJECTIVE TYPE QUESTIONS))|69 Videos

  • COMMUNICATION SYSTEMS

    AAKASH INSTITUTE ENGLISH|Exercise ASSIGNMENT SECTION D (Assertion-Reason)|10 Videos

  • DUAL NATURE OF RADIATION AND MATTER

    AAKASH INSTITUTE ENGLISH|Exercise ASSIGNMENT (SECTION-D)|10 Videos

Similar Questions

Explore conceptually related problems

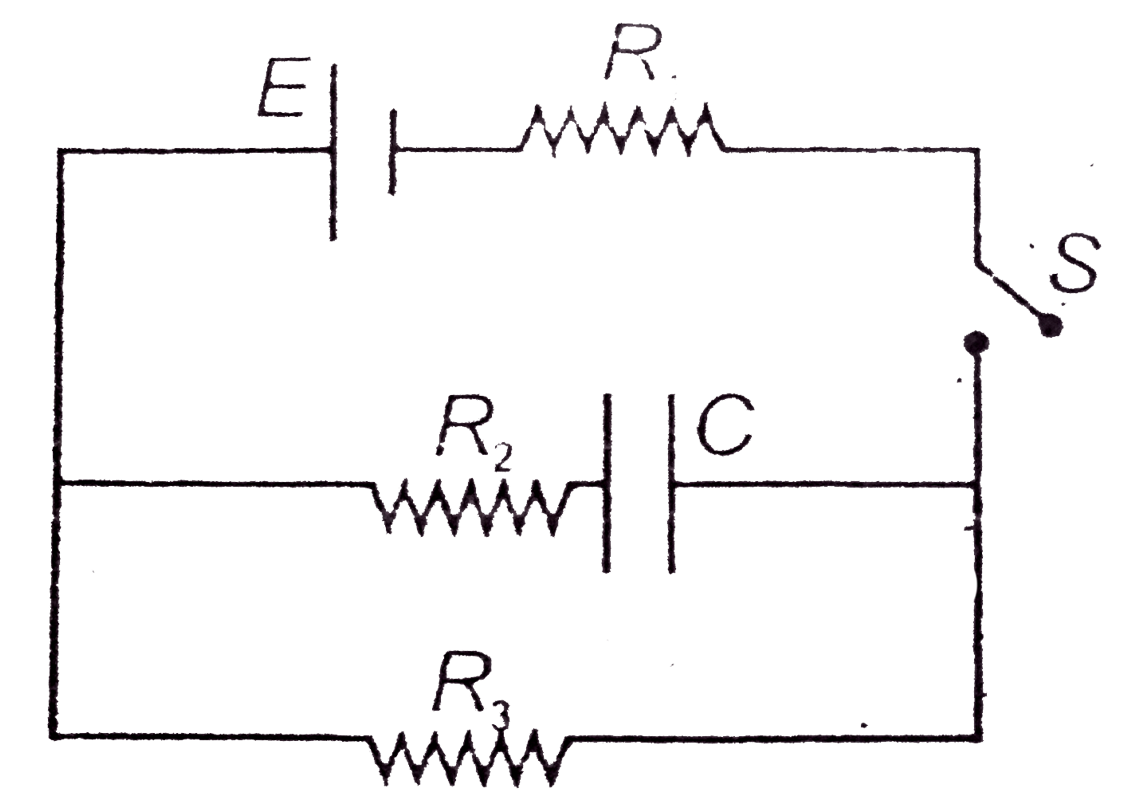
For the circuit shown in figure, find (a) the initial current through each resistor (b) steady state current through each resistor (c) final energy stored in the capacitor (d) time constant of the circuit when switch is opened.

A coil of inductance 2 H and resistance 10 Omega are in a series circuit with an open key and a cell of constant 100 V with negligible resistance. At time i = 0 , the key is closed. Find (a) the time constant of the circuit. (b) the maximum steady current in the circuit. (c) the current in the circuit at f =1 s .

The current in a discharging LR circuit without the battery drops from 2.0 A to 1.0A in 0.10 s. (a) find the time constant of the circuit. (b) if the inductance of the circuit is 4.0 H, what is its resistance?

The reading of an ammeter in the circuit (i) I when key K_(1) closed key K_(2) is open (ii) I//2 when both keys K_(1) and K_(2) are closed Find the expression for the resistance of X in terms of the resistances of R and S

The magnetic field in the cylindrical region shown in increases at a constant rate of 20.0 mT/s. Each side of the square loop abcd and defa has a length of 1.00 cm and a resistance of 4.00 Omega . Find the current (magnitude and sense) in the wire ad if (a) the switch S_1 is closed but S_2 is open, (b) S_1 is open but S_2 is closed, (c) both S_1 and S_2 are open and (d) both S_1 and S_2 are closed.

The time constant, for charging of capacitor C, when switch S is closed as shown in the figure , is

Consider the circuit shown in the figure. (a) Find the current i flowing through the circuit when the key K_(1) is open and K_(2) is closed. (b) Find the net charge on the capacitor when K_(1) is open & K_(2) is.closed and also when K_(1) & K_(2) both are closed. (c) What is the change in the current'i, when K_(1) is closed

Consider the circuit shown below. When switch S_(1) is closed, let I be the current at time t, then applying Kirchhoff's law E-iR-L (di)/(dt) = 0 or int_(0)^(i) (di)/(E-iR) = 1/L int_(0)^(1) dt i=E/R (1-e^(-R/l *t)) L/R = time constant of circuit When current reaches its steady value (=i_(0) , open S_(1) and close S_(2) , the current does reach to zero finally but decays expnentially. The decay equation is given as i=i_(0)e^(-R/L *T) ). When a coil carrying a steady current is short circuited, the current decreases in it eta times in time t_(0) . The time constant of the circuit is

In the circuit shown, the capacitor initially charged with a 12V batteryy, when switch S_(1) is open and switch S_(2) is closed. The maximum value of current in the circuit when S_(2) is opened and S_(2) is closed is

Consider the circuit shown in figure.(a) find the current through the battery a long time after the switch S is closed. (b) Suppose the switch is again opened at t = 0. What is the time constant of the discharging circuit? (c ) Find t current through the inductor after one time constant.