A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
CURRENT ELECTRICITY
AAKASH INSTITUTE ENGLISH|Exercise ASSIGNMENT SECTION-D( LINKED COMPREHENSION TYPE QUESTIONS)|3 VideosCURRENT ELECTRICITY
AAKASH INSTITUTE ENGLISH|Exercise ASSIGNMENT SECTION-D( LINKED COMPREHENSION TYPE QUESTIONS) Comprehension - II|5 VideosCURRENT ELECTRICITY
AAKASH INSTITUTE ENGLISH|Exercise ASSIGNMENT SECTION-B(OBJECTIVE TYPE QUESTION ))|44 VideosCOMMUNICATION SYSTEMS
AAKASH INSTITUTE ENGLISH|Exercise ASSIGNMENT SECTION D (Assertion-Reason)|10 VideosDUAL NATURE OF RADIATION AND MATTER
AAKASH INSTITUTE ENGLISH|Exercise ASSIGNMENT (SECTION-D)|10 Videos
Similar Questions
Explore conceptually related problems
AAKASH INSTITUTE ENGLISH-CURRENT ELECTRICITY-ASSIGNMENT SECTION-C(OBJECTIVE TYPE QUESTION ))
- Consider the following arrangement of resistors . The currents in vari...
Text Solution
|
- A cell supplies a current of 2A to an exertnal resistance of 2Omega a...
Text Solution
|
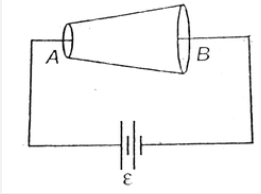
- Figure shows a conical conducting wire connected to a source of emf. L...
Text Solution
|
- A resistance R(1) is connected to a source of constant voltage . On co...
Text Solution
|
- In the circuit shown, current in different branches are marked. Select...
Text Solution
|
- In the circuit shown, readint of galvanometer is zero. Select the corr...
Text Solution
|
- If all the resistors are identical , select the correct alternative (s...
Text Solution
|
- A current enters from A and leaves at B through the network shown. Sel...
Text Solution
|
- Consider the circuit shown. Which of the following values is // are c...
Text Solution
|
- A capacitor is charged to a potential difference of 100 V and is then ...
Text Solution
|
- In the circuit shown, the switch is closed at t=0. Select the correct...
Text Solution
|
- An uncharged capacitor is connected to an ideal battery through a resi...
Text Solution
|
- The figure shows two capacitors connected in parallel with two resista...
Text Solution
|