Home
Class 9
MATHS
ABC and BDE are two equilateral trian...

ABC and BDE are two equilateral triangles such that D is the mid- point of BC. If AB = 20 cm . Find the area of the shaded portions [ Take ` sqrt3 = 1.73]`

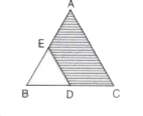
Text Solution

Verified by Experts

The correct Answer is:
` 129 . 75 cm ^(2)`
Promotional Banner

Topper's Solved these Questions

  • CHAPTER REVISION (STAGE 2)

    ICSE|Exercise SOLIDS |7 Videos

  • CHAPTER REVISION (STAGE 2)

    ICSE|Exercise TRIGONOMETRY |36 Videos

  • CHAPTER REVISION (STAGE 2)

    ICSE|Exercise MEAN AND MEDIAN |4 Videos

  • AREA THEOREMS

    ICSE|Exercise Exercies 16(C )|22 Videos

  • CHAPTERWISE REVISION (STAGE 1)

    ICSE|Exercise Graphical solution |10 Videos

Similar Questions

Explore conceptually related problems

ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, ar (DeltaBDE) = (1)/(4) ar (DeltaABC) .

Tick the correct answer and justify:ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is (A) 2:1 (B) 1:2 (C) 4:1 (D) 1:4

In fig, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that: (i) ar(BDE)= 1/4 ​ ar(ABC) (ii) ar(BDE)= 1/2 ​ ar(BAE)

ABC is an equilateral triangle inscribed in a circle of radius 4 cm. Find the area of the shaded portion.

In Fig. an equilateral triangle A B C of side 6 cm has been inscribed in a circle. Find the area of the shaded region. (Take pi=3. 14 )

The side of an equilateral triangle is 6sqrt(3) cm. Find the area of the triangle. [Take sqrt(3)=1.732 ]

In an equilateral triangle ABC , D is the mid-point of AB and E is the mid-point of AC. Find the ratio between ar ( triangleABC ) : ar(triangleADE)

In the following figure, a rectangle ABCD encloses three circles. If BC = 14 cm, find the area of the shaded portion. (Take a pi= 3(1)/(7) )

The area of the equilateral triangle is 20sqrt3cm^(2) whose each side is 8 cm.

The given figure shows a right angled triangle ABC and an equilateral triangle BCD. Find the area of the shaded portion.