Topper's Solved these Questions
CHAPTERWISE REVISION EXERCISE
ICSE|Exercise CHAPTERWISE REVISION EXERCISE (LOCI)|7 VideosCHAPTERWISE REVISION EXERCISE
ICSE|Exercise CHAPTERWISE REVISION EXERCISE (CIRCLES)|9 VideosCHAPTERWISE REVISION EXERCISE
ICSE|Exercise CHAPTERWISE REVISION EXERCISE (EQUATIONS OF STRAIGHT LINES)|12 VideosBANKING (RECURRING DEPOSIT ACCOUNTS)
ICSE|Exercise QUESTIONS|7 VideosCIRCLES
ICSE|Exercise EXERCISE 17( C ) |28 Videos
Similar Questions
Explore conceptually related problems
ICSE-CHAPTERWISE REVISION EXERCISE-CHAPTERWISE REVISION EXERCISE (SIMILARITY)
- M is the mid-point of a line segment AB, AXB and MYB are equilateral t...
Text Solution
|
- In the given figure, if AC=3cm and CB=6cm, find the length of CR.
Text Solution
|
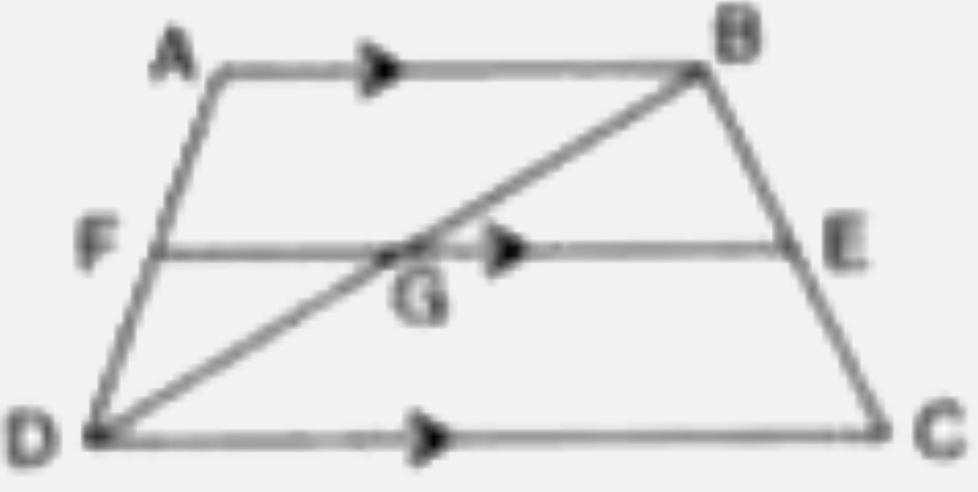
- The given figure shows a trapezium in which AB is parallel to DC and d...
Text Solution
|
- The given figure shows a trapezium in which AB is parallel to DC and d...
Text Solution
|
- The given figure shows a trapezium in which AB is parallel to DC and d...
Text Solution
|
- The given figure shows a trapezium in which AB is parallel to DC and d...
Text Solution
|
- A model of a ship is made to a scale of 1:160. Find: the length of ...
Text Solution
|
- A model of a ship is made to a scale of 1:160. Find: the area of the...
Text Solution
|
- A model of a ship is made to a scale of 1:160. Find: the volume of t...
Text Solution
|
- In trapezium ABCD, AB//DC and DC=2 AB. EF, drawn parallel to AB cuts A...
Text Solution
|