A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-TEST PAPERS-PHYSICS
- A particle is moving in a straight line. Its displacement at any insta...
Text Solution
|
- A particle starts its motion from rest under the action of a constant ...
Text Solution
|
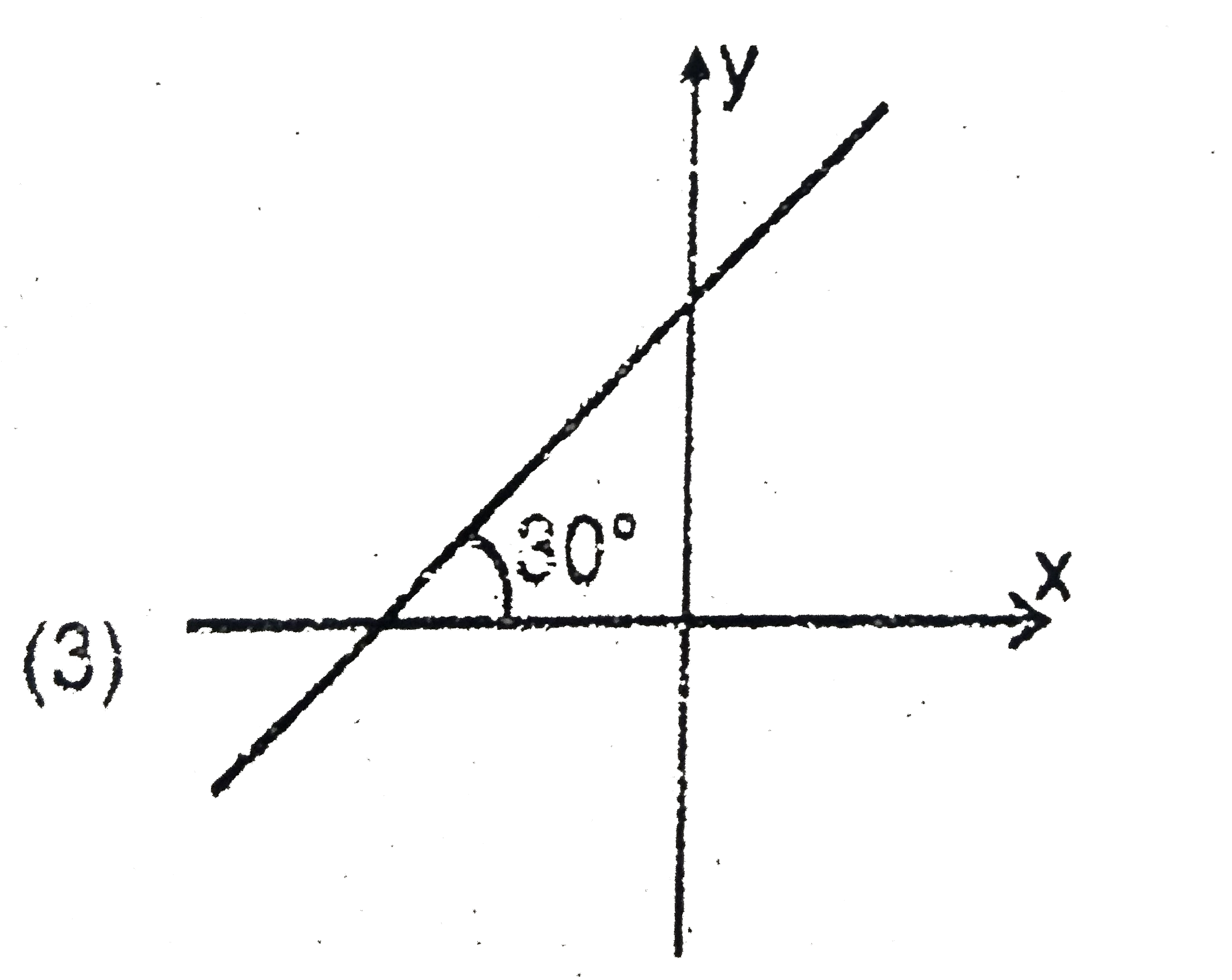
- The graph of straight line y = sqrt(3)x + 2sqrt(3) is :
Text Solution
|
- If f(x) = x^(2) and g(x) = (1)/(x^(3)). Then the value of (f(x)+g(x))/...
Text Solution
|
- If two forces each of magnitude 20N, are acting on a particle such tha...
Text Solution
|
- A particle is moving with constant speed V m//s along the circumferenc...
Text Solution
|
- Drops of water fall at regular intervals from the roof of a building o...
Text Solution
|
- The position vector of a particle is given by vec r = (2t hati+5t^(2)h...
Text Solution
|
- The velocity displacement graph of a particle is shown in figure. The...
Text Solution
|
- The position of a particle is defined by vec r = 2sin((pi)/(4))t hati ...
Text Solution
|
- The slope of the curve y = x^(3) - 2x+1 at point x = 1 is equal to :
Text Solution
|
- A particle is moving on a straight line with velocity (v) as a functio...
Text Solution
|
- A particle is moving on a straight line with velocity (v) as a functio...
Text Solution
|
- A particle is moving on a straight line with velocity (v) as a functio...
Text Solution
|
- A body which was released from rest, slides down on an inclined plane ...
Text Solution
|
- Two particles A and B are located at point (0m, 50m) at t = 0. The par...
Text Solution
|
- A particle is projected at t = 0 with velocity u at angle theta with t...
Text Solution
|
- System shown in figure is released from rest. Pulley and spring is mas...
Text Solution
|
- A stone is projected at angle 45^(@) with the horizontal (x- axis) as ...
Text Solution
|
- A particle is moving with a constant acceleration veca = hati-2hatj+2h...
Text Solution
|