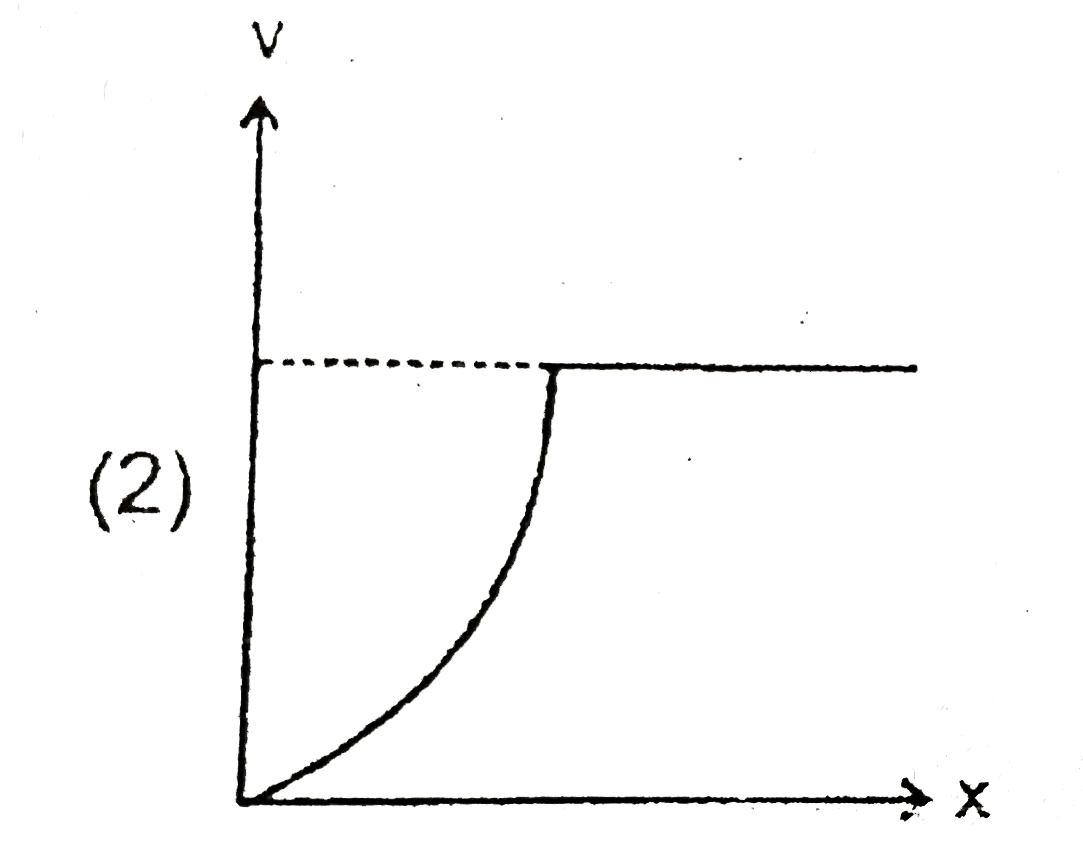
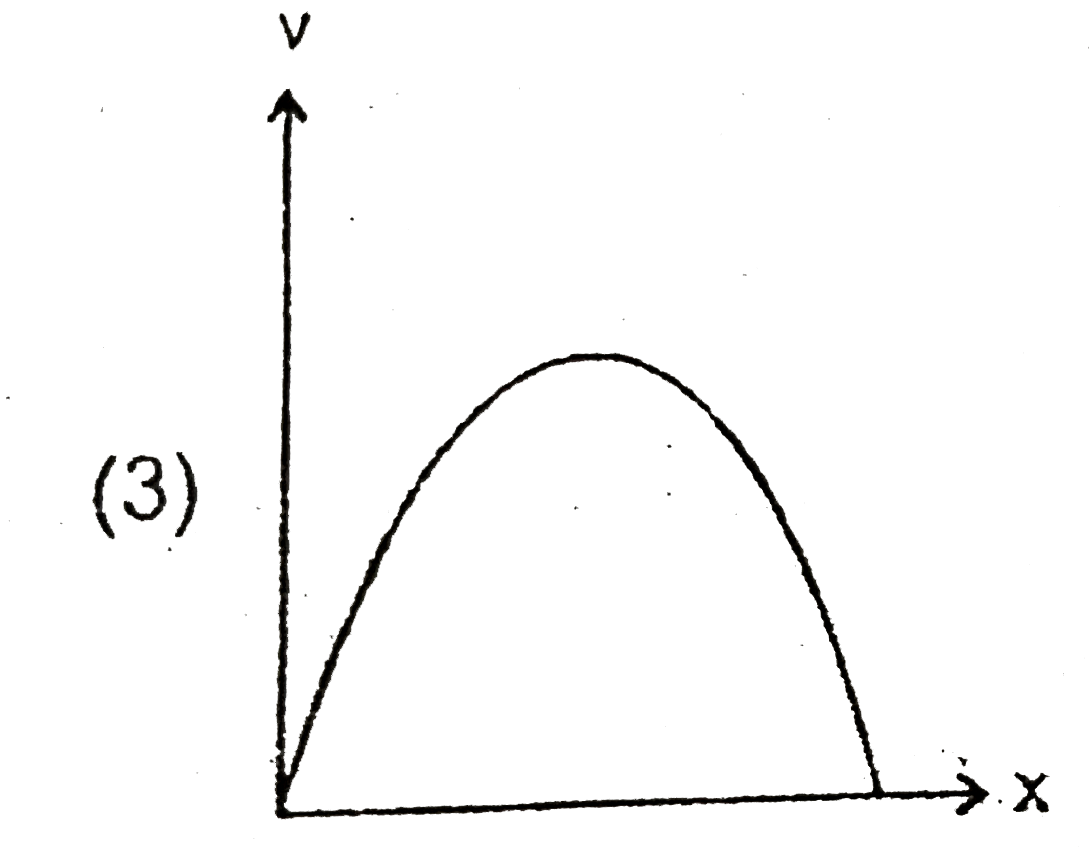
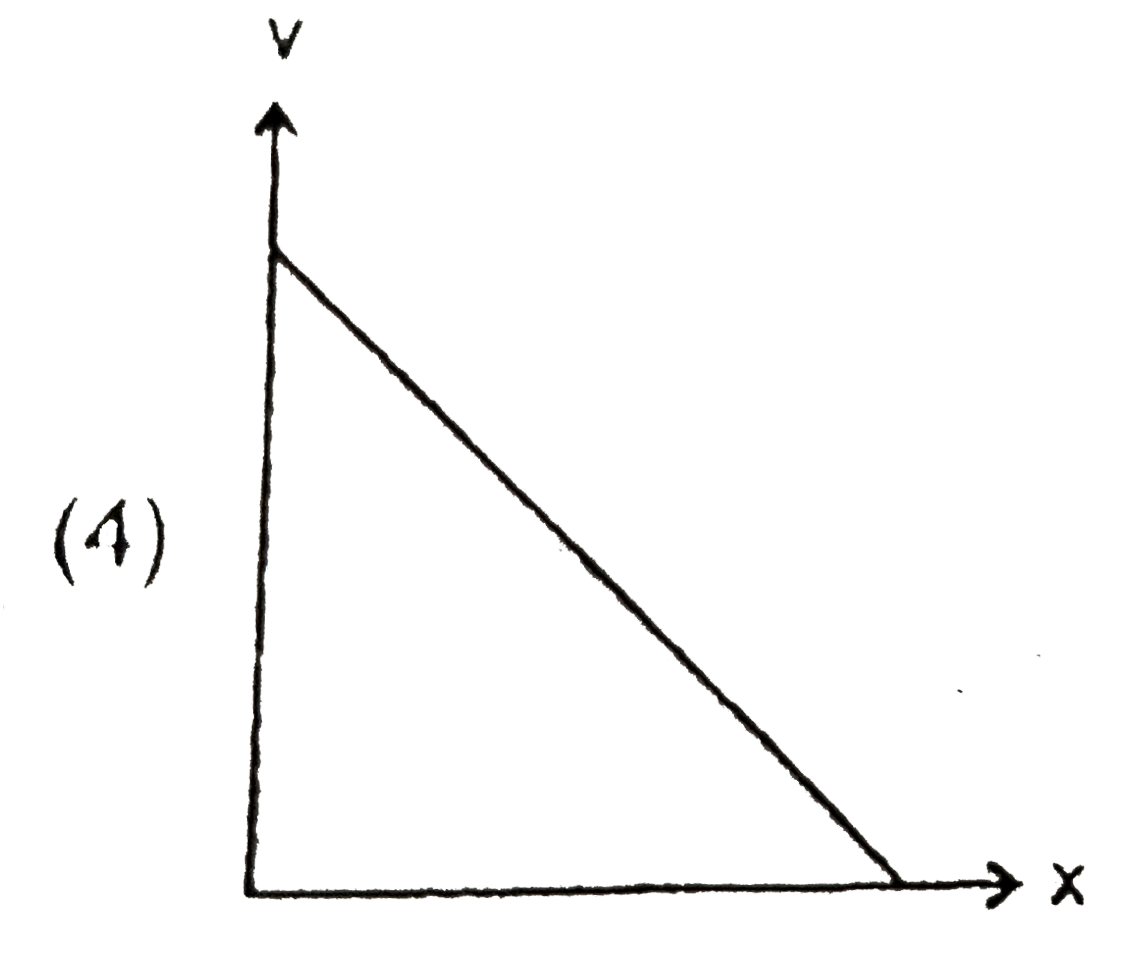
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
RESONANCE ENGLISH-TEST PAPERS-PHYSICS
- A particle is moving on a straight line with velocity (v) as a functio...
Text Solution
|
- A particle is moving on a straight line with velocity (v) as a functio...
Text Solution
|
- A body which was released from rest, slides down on an inclined plane ...
Text Solution
|
- Two particles A and B are located at point (0m, 50m) at t = 0. The par...
Text Solution
|
- A particle is projected at t = 0 with velocity u at angle theta with t...
Text Solution
|
- System shown in figure is released from rest. Pulley and spring is mas...
Text Solution
|
- A stone is projected at angle 45^(@) with the horizontal (x- axis) as ...
Text Solution
|
- A particle is moving with a constant acceleration veca = hati-2hatj+2h...
Text Solution
|
- A block of mass 10kg is placed on rough inclined plane of variable ang...
Text Solution
|
- A roller coaster car travels down the helical path at constant speed s...
Text Solution
|
- For ground to ground projectile, time take by a particle to ge point ...
Text Solution
|
- A box of mass 10 kg is lowered with a downward acceleration 4 m//s^(2)...
Text Solution
|
- Rain is falling with constant and uniform velocity v at angle 37^(@) v...
Text Solution
|
- A particle of mass m is moving with constant velocity v parallel to th...
Text Solution
|
- A particle is ejected from the tube at A with a velocity V at an angle...
Text Solution
|
- A small block of mass m os takes slowly up a fixed hemisphere from P t...
Text Solution
|
- The acceleration of block 'C' is equal to (g)/(12)m//s^(2) where g is ...
Text Solution
|
- A slab of 40 kg lying on a frictionales floor and a block of 10 kg res...
Text Solution
|
- The acceleration of a particle moving in straight line is defined by t...
Text Solution
|
- If XYZ is an equilateral triangle. Then the resultant of the three for...
Text Solution
|