Home
Class 11
PHYSICS
Find the magnitude of the unknown forces...

Find the magnitude of the unknown forces `X` and `Y` if sum of all forces is zero.

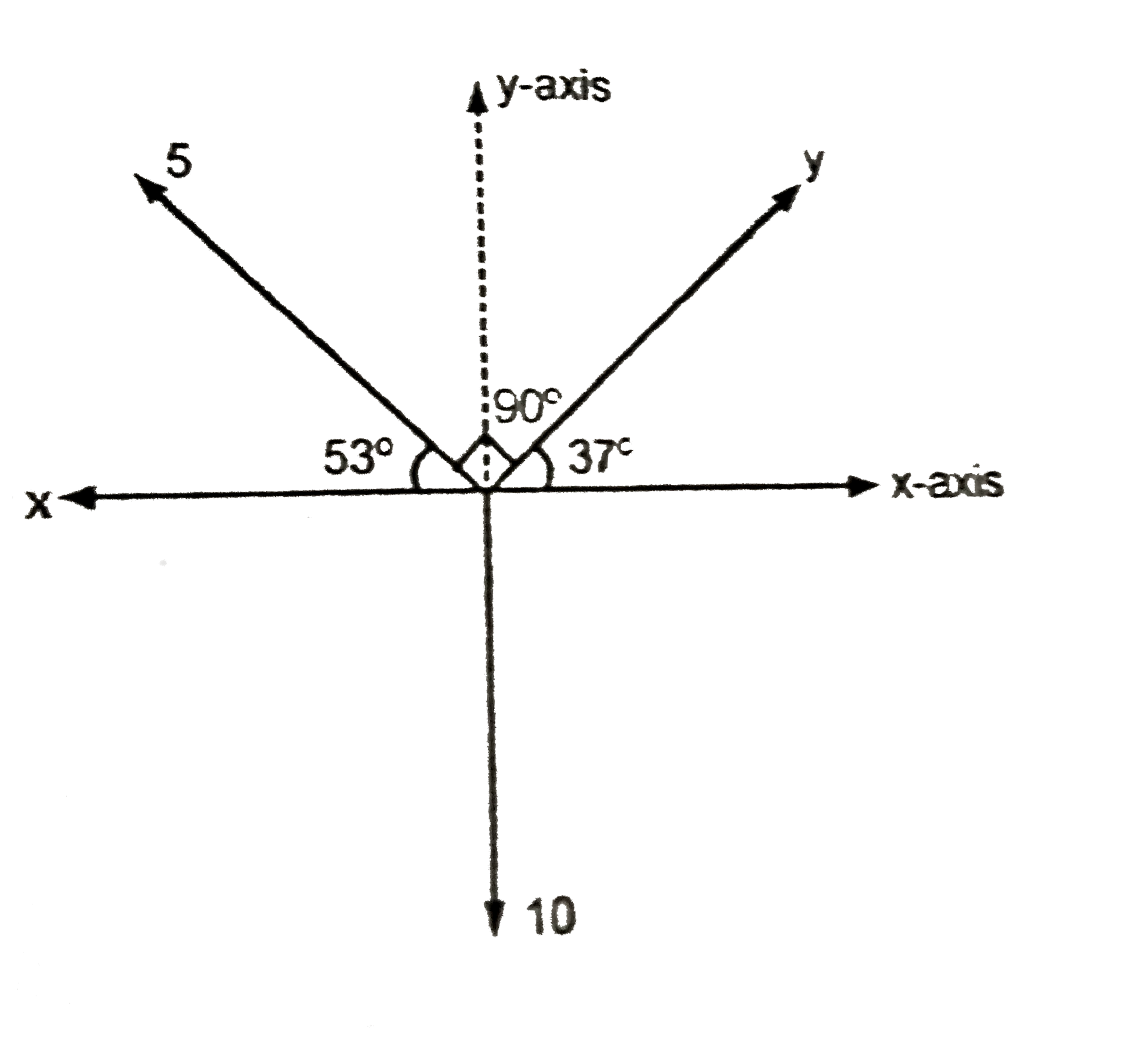
Text Solution

Verified by Experts

The correct Answer is:
`(5,10)`

`Sigmavec(F)=0`
`rArr (y cos 37^(@)hat(i)+y sin37^(@)hat(j))+(5cos53^(@)(-hat(i))+5sin53^(@)hat(j))+(x(-hat(i)))+10(-hat(j)))=0`
`rArr((4y)/(5)-3-x)hat(i)+((3y)/(5)+4-10)hat(j)=0hat(i)+0hat(j)`
Comparting coefficients of `hat(i) & hat (j)` both sided - `(4y)/(5)-x=3` .......`(i)`
`(3y)/(5)=6 rArr y=10`
Putting `8-x=3rArrx=5`
Promotional Banner

Topper's Solved these Questions

  • DAILY PRACTICE PROBLEMS

    RESONANCE ENGLISH|Exercise Dpp no 10 physics|8 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE ENGLISH|Exercise Dpp no 11 physics|6 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE ENGLISH|Exercise DPP 8 PHYSICS|7 Videos

  • CURRENT ELECTRICITY

    RESONANCE ENGLISH|Exercise Exercise|53 Videos

  • ELASTICITY AND VISCOCITY

    RESONANCE ENGLISH|Exercise Advanced Level Problems|9 Videos

Similar Questions

Explore conceptually related problems

Find the magnitudes of the unknown forces if the sum of all forces is zero (figure)

Find the magnitude of the resultant of shown forces :-

Find the values of the unknowns x and y in the following diagrams

Two forces with equal magnitudes F act on a body and the magnitude of the resultant force is F /3. The angle between the two forces is

Two forces of magnitudes P and Q are inclined at an angle (theta) . The magnitude of their resultant is 3Q. When the inclination is changed to (180^(@)-theta) , the magnitude of the resultant force becomes Q. Find the ratio of the forces.

Let F,F_N and f denote the magnitudes of the contact force, normal force and the friction exerted by one surface on the other kept in contact. If none of these is zero,

Assertion: Magnitude of the contact force is always greater than the magnitude of frictional force. Reason: Contact force is the resultant of the friction force and normal reaction.

The sum of the magnitudes of two forces acting at a point is 18 and the magnitude of their resultant is 12. If the resultant is at 90^(@) with the force of smaller magnitude, What are the magnitudes of forces?

The sum of the magnitudes of two forces acting at a point is 18 and the magnitude of their resultant is 12. If the resultant is at 90^(@) with the force of smaller magnitude, What are the magnitudes of forces?

The sum of magnitudes of two forces acting at a point is 16 N . If the resultant force is 8 N and its direction is perpendicular to smaller force, then the forces are :-