A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DAILY PRACTICE PROBLEMS
RESONANCE ENGLISH|Exercise dpp 27|3 VideosDAILY PRACTICE PROBLEMS
RESONANCE ENGLISH|Exercise dpp 28|7 VideosDAILY PRACTICE PROBLEMS
RESONANCE ENGLISH|Exercise dpp 25|5 VideosCURRENT ELECTRICITY
RESONANCE ENGLISH|Exercise Exercise|53 VideosELASTICITY AND VISCOCITY
RESONANCE ENGLISH|Exercise Advanced Level Problems|9 Videos
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-DAILY PRACTICE PROBLEMS-dpp 26
- Two men of masses m and m//2 starts climbing up on two masseless strin...
Text Solution
|
- Two particles at a distance 5 m apart, are thrown towards each other ...
Text Solution
|
- A particle is projected from a point (0,1) of Y-axis (assume + Y direc...
Text Solution
|
- System shown in figure is in equilibrium, find the magnitude of net ch...
Text Solution
|
- A cylinder rests in a supporting carriage as shown. The side AB of car...
Text Solution
|
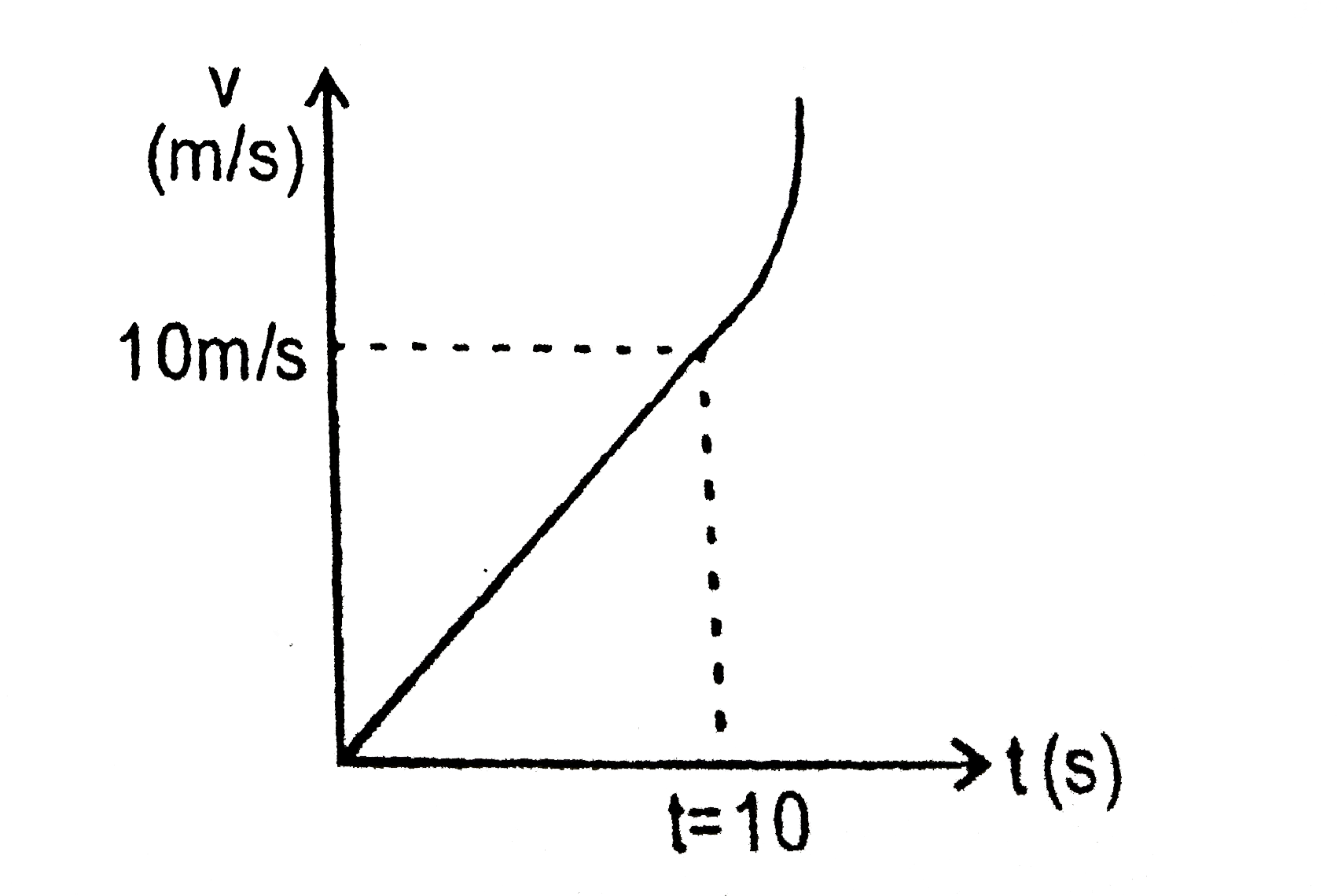
- A particle is moving in a straight line as : a=1m//s^(2) 0letle10 ...
Text Solution
|
- A force F is applied on block A of mass M so that the tension in light...
Text Solution
|
- During a rainy day, rain is falling vertically with a velocity 2 ms^-1...
Text Solution
|