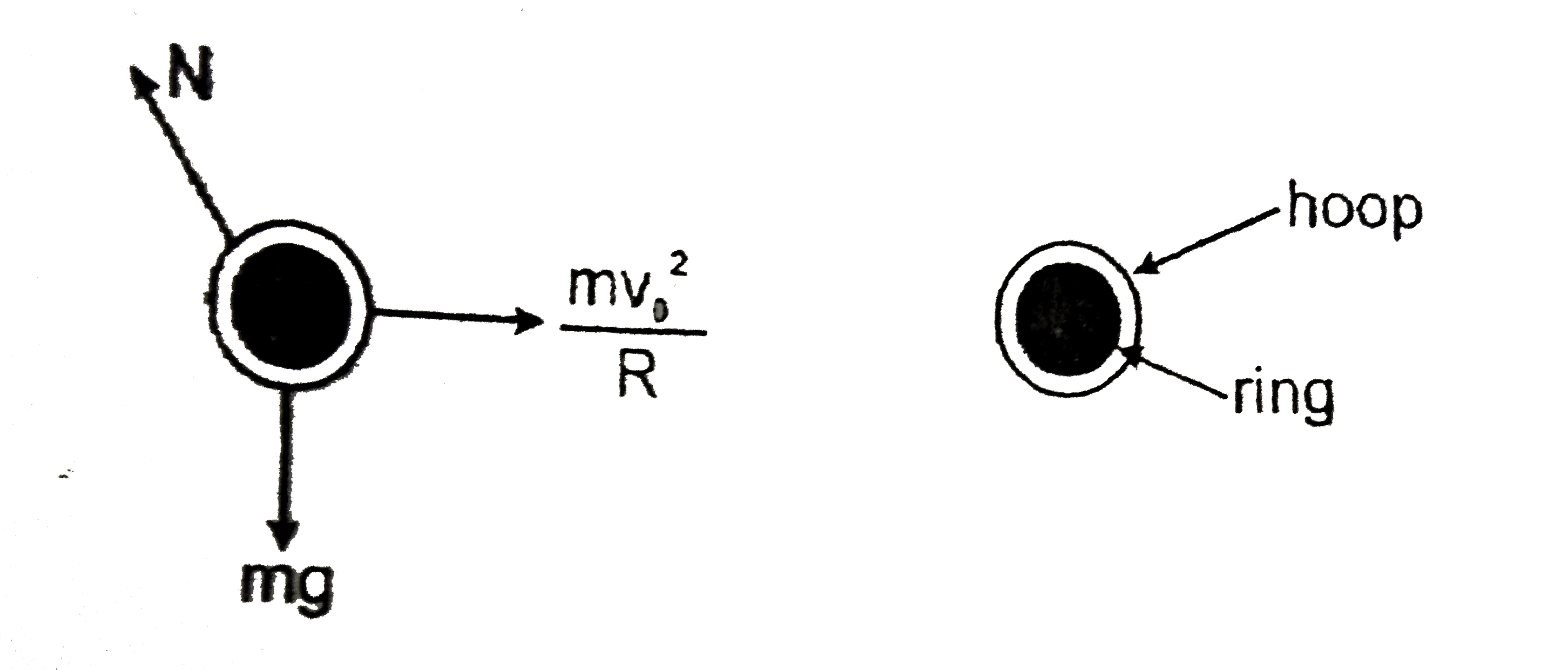Home
Class 11
PHYSICS
A small hoop of mass m is given an initi...

A small hoop of mass `m` is given an initial velocity of magnitude `v_(0)` on the horizontal circular ring of radius `'r'`. If the coefficient of kinetic friction is `mu_(k)` the tangential acceleration of the hoop immediately after is release is `(` assume the horizontal ring to be fixed and not in contact with any supporting surface `)`

A

`mu_(k)g`

B

`mu_(k)(v_(0)^(2))/(r)`

C

`mu_(k)sqrt(g^(2)+(v^(2))/(r))`

D

`mu_(k)sqrt(g^(2)+(v_(0))/(r^(2)))`

Text Solution

Verified by Experts

The correct Answer is:
D
The free body diagram of hoop is
`:. `The normal reaction `N=sqrt(m^(2)g^(2)+(m^(2)v_(0)^(4))/r^(2))`
`:. ` Frictional force `=mu_(k)N=mu_(k)sqrt(m^(2)g^(2)+(m^(2)v_(0)^(4))/(r^(2)))`

`:. ` tangentail acceleration `=(mu_(k)N)/(m)`
`=mu_(k)sqrt(g^(2)+(v_(0)^(4))/(r^(2)))`
Promotional Banner

Topper's Solved these Questions

  • DAILY PRACTICE PROBLEMS

    RESONANCE ENGLISH|Exercise dpp 52|7 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE ENGLISH|Exercise dpp 53|5 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE ENGLISH|Exercise DPP 50|5 Videos

  • CURRENT ELECTRICITY

    RESONANCE ENGLISH|Exercise Exercise|53 Videos

  • ELASTICITY AND VISCOCITY

    RESONANCE ENGLISH|Exercise Advanced Level Problems|9 Videos

Similar Questions

Explore conceptually related problems

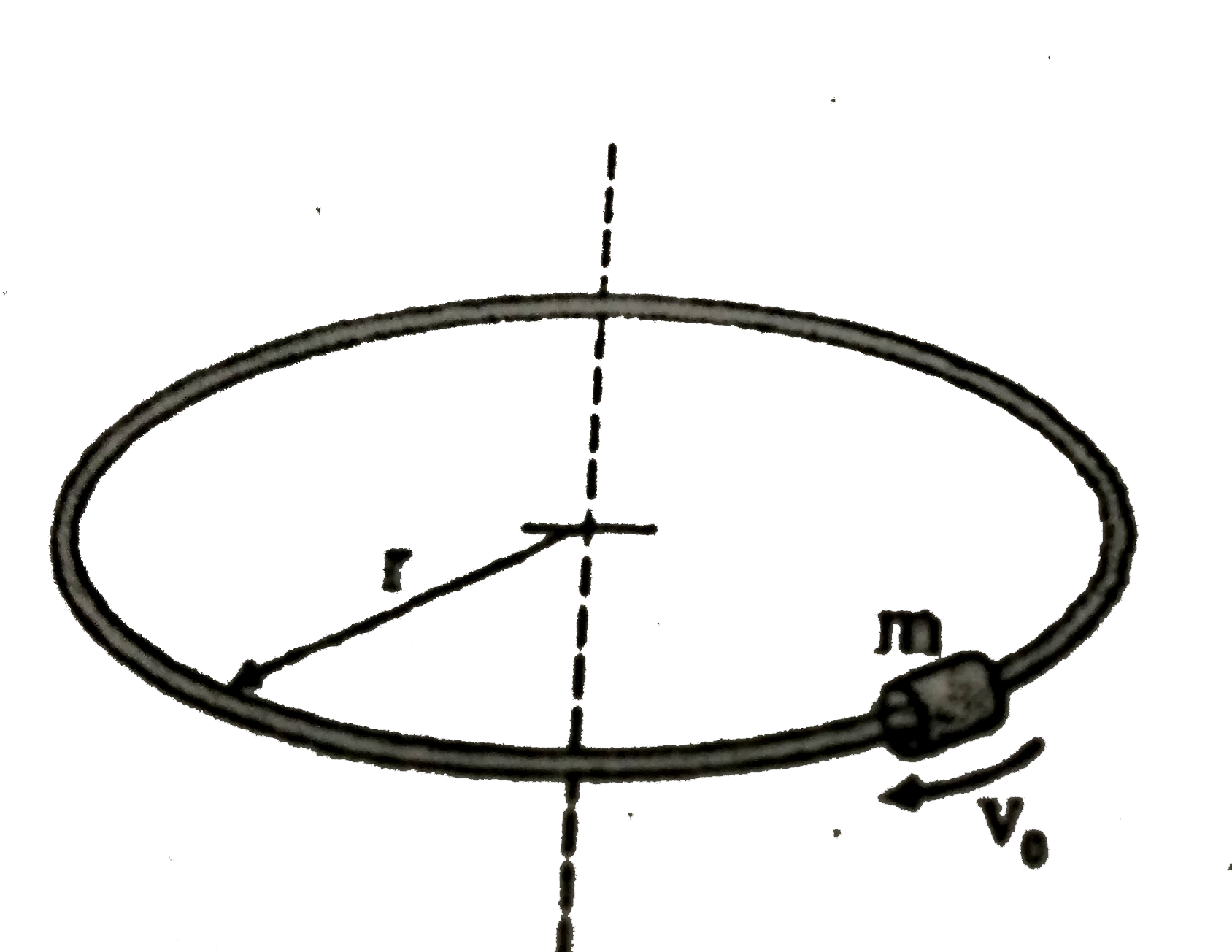
Choose the correct option: A small collar of mass m is given an initial velocity of magnitude v_(0) on the horizontal circular track fabricated from a slender rod. If the coefficient of kinetic friction is mu_(K) , determine the distance traveled before the collar comes to rest. (Recognize that the friction force depends on the net normal force).

A ring of mass m sliding on a smooth surface with velocity v_(0) enters rough surface with coefficient of kinetic friction mu_(k) , then

A block of mass m moving with a velocity v_(0) on a rough horizontal surface from x=0 coefficient of friction is given by mu=mu_(0)+ax . Find the kinetic energy of the block as function of x before it comes to rest.

A ring of radius R is rotating with an angular speed omega_0 about a horizontal axis. It is placed on a rough horizontal table. The coefficient of kinetic friction is mu_k . The time after it starts rolling is.

A block of mass m is pushed with a velocity v_(0) along the surface of a trolley car of mass M . If the horizontal ground is smooth and the coefficient of kinetic friction between the block of plank is mu . Find the minimum distance of relative sliding between the block and plank.

A hoop of radius r mass m rotating with an angular velocity omega_(0) is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it cases to slip ?

A ring of radius R is first rotated with an angular velocity omega and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is mu . Time after which its angular speed is reduced to half is

A car starts rest, on a horizontal circular road of radius R, the tangential acceleration of the car is a. The friction coefficient between the road and the tyre is mu Find the speed at which car will skid and also find the distance after travelling it skids.

A solid ball of mass m and radius r spinning with angular velocity omega falls on a horizontal slab of mass M with rough upper surface (coefficient of friction mu ) and smooth lower surface. Immediately after collision the normal component of velocity of the ball remains half of its value just before collision and it stops spinning. Find the velocity of the sphere in horizontal direction immediately after the impact (given: Romega= 5 ).

A block B is pushed momentarily along a horizontal surface with an initial velocity v . If mu is the coefficient of sliding friction between B and the surface, block B will come to rest after a time: