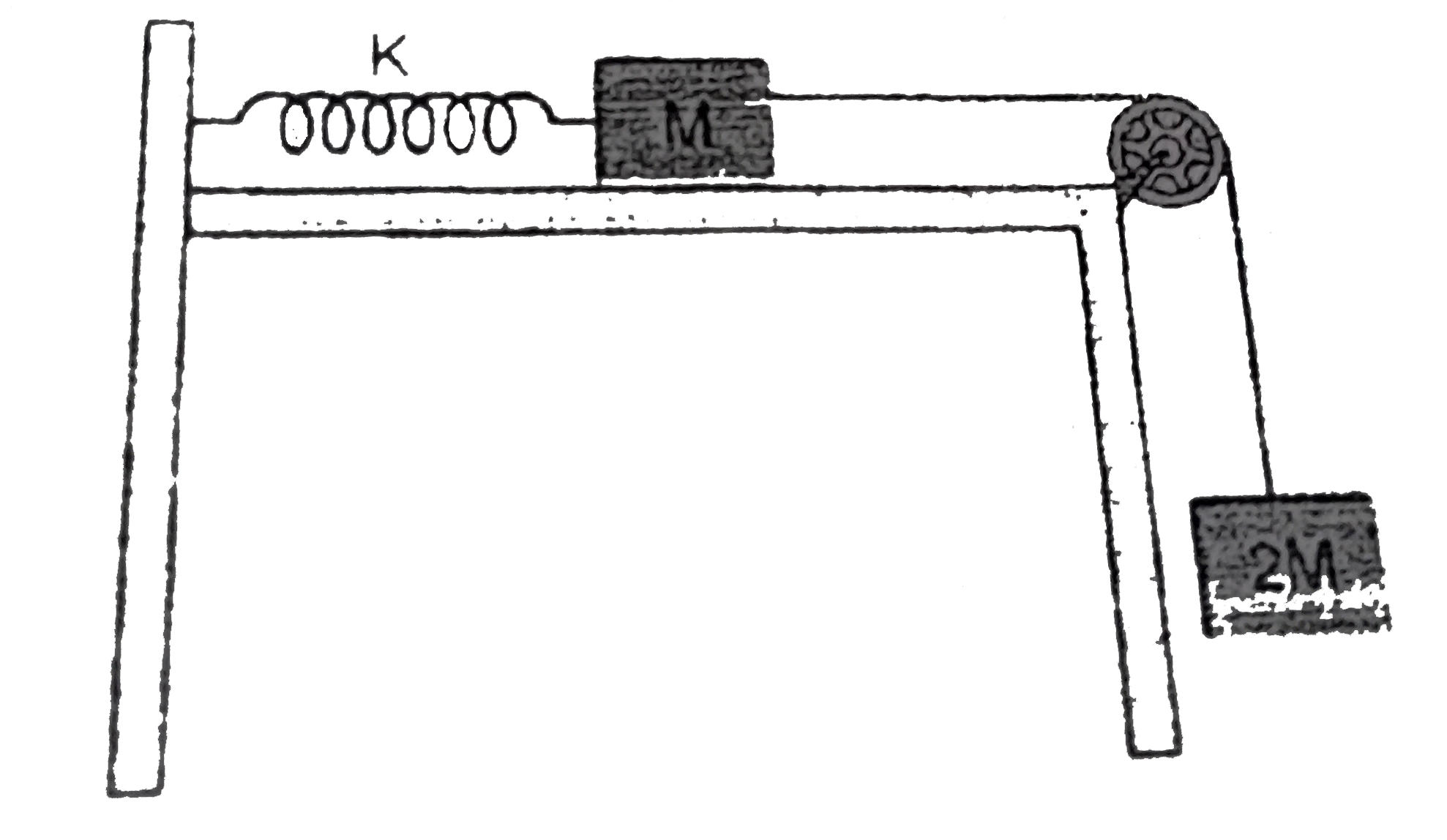
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DAILY PRACTICE PROBLEMS
RESONANCE ENGLISH|Exercise dpp 53|5 VideosDAILY PRACTICE PROBLEMS
RESONANCE ENGLISH|Exercise dpp 54|8 VideosDAILY PRACTICE PROBLEMS
RESONANCE ENGLISH|Exercise dpp 51|7 VideosCURRENT ELECTRICITY
RESONANCE ENGLISH|Exercise Exercise|53 VideosELASTICITY AND VISCOCITY
RESONANCE ENGLISH|Exercise Advanced Level Problems|9 Videos
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-DAILY PRACTICE PROBLEMS-dpp 52
- Eight solid uniform cubes of edge l are stacked together to form a sin...
Text Solution
|
- A uniform rod of mass M and length L falls when it is made to stand on...
Text Solution
|
- A man places a chain (of mass m and length l) on a table slowly. Initi...
Text Solution
|
- The potential energy (in SI units) of a particle of mass 2kg in a cons...
Text Solution
|
- A penguin of mass m stands at the right edge of a sled of mass 3m and ...
Text Solution
|
- Two blocks, of masses M and 2M are connected to a light spring of spri...
Text Solution
|
- Two blocks A and B of mass m and 2m are connected by a massless sprin...
Text Solution
|