Home
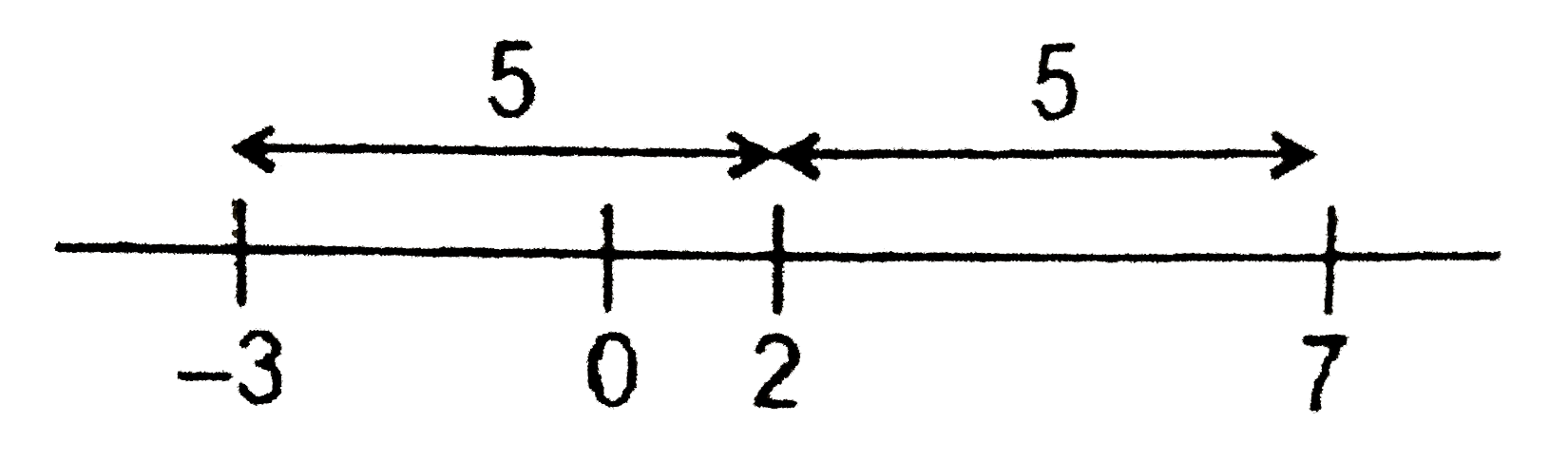
Class 11
PHYSICS
A particle moving on x - axis has potent...

A particle moving on x - axis has potential energy `U = 2 - 20x + 5x^(2)` joule along x - axis. The particle is relesed at `x = -3`. The maximum value of `x` will be (`x` is in metre)

A

`5m`

B

`3m`

C

`7m`

D

`8m`

Text Solution

Verified by Experts

The correct Answer is:
C
`U=2-20x+5x^(2)`
`F=-(dU)/(dx)=20-10x`
At equilibrium position `,F=0`
`20-10x=0`
`rArr x=2`
Since particle is released at `x=-3` , therefore amplitude of particle is 5 .

It will osciallte about `x=2` with an amplitude of 5.
`:. `maximum value of `x` will be 7.
Promotional Banner

Topper's Solved these Questions

  • DAILY PRACTICE PROBLEMS

    RESONANCE ENGLISH|Exercise dpp73|4 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE ENGLISH|Exercise dpp 74|7 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE ENGLISH|Exercise dpp 71|8 Videos

  • CURRENT ELECTRICITY

    RESONANCE ENGLISH|Exercise Exercise|53 Videos

  • ELASTICITY AND VISCOCITY

    RESONANCE ENGLISH|Exercise Advanced Level Problems|9 Videos

Similar Questions

Explore conceptually related problems

A particle moves along the X-axis as x=u(t-2s)=at(t-2)^2 .

A particle moves along the X-axis as x=u(t-2 s)+a(t-2 s)^2 .

Position of particle moving along x-axis is given as x=2+5t+7t^(2) then calculate :

A particle is moving along the x-axis with an acceleration a = 2x where a is in ms^(–2) and x is in metre. If the particle starts from rest at x=1 m, find its velocity when it reaches the position x = 3.

Velocity of particle moving along x-axis is given as v = ( x^(3) - x^(2) + 2) m // sec. Find the acceleration of particle at x=2 meter.

For a particle moving along x- axis, speed must be increasing for the following graph :

A particle of mass 4 kg moves along x axis, potential energy ( U ) varies with respect to x as U = 20 + ( x-4)^(2) , maximum speed of paritcle is at

A particle is moving along the x-axis whose acceleration is given by a= 3x-4 , where x is the location of the particle. At t = 0, the particle is at rest at x = 4//3m . The distance travelled by the particles in 5 s is

A particle is moving along x -axis. Its velocity v with x co-ordinate is varying as v=sqrt(x) . Then

A single conservative fore F_(x) acts on a 2kg particle that moves along the x-axis. The potential energy is given by. U =(x-4)^(2)-16 Here, x is in metre and U in joule. At x =6.0 m kinetic energy of particle is 8 J find . (a) total mechanical energy (b) maximum kinetic energy (c) values of x between which particle moves (d) the equation of F_(x) as a funcation is zero (e) the value of x at which F_(x) is zero .