Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DAILY PRACTICE PROBLEM
RESONANCE ENGLISH|Exercise DPP No.27|20 VideosDAILY PRACTICE PROBLEM
RESONANCE ENGLISH|Exercise DPP No.28|9 VideosDAILY PRACTICE PROBLEM
RESONANCE ENGLISH|Exercise DPP No.25|20 VideosCURRENT ELECTRICITY
RESONANCE ENGLISH|Exercise High Level Problems (HIP)|19 VideosELECTRO MAGNETIC WAVES
RESONANCE ENGLISH|Exercise Exercise 3|27 Videos
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-DAILY PRACTICE PROBLEM-DPP No.26
- A small particle of mass m is released from rest from point A inside ...
Text Solution
|
- Figure shows two block A and B, each having a mass of 320 g connected ...
Text Solution
|
- The potential energy varphi, in joule, of a particle of mass 1kg, movi...
Text Solution
|
- Three charges are placed as shown in fig. the magnitude of q(1) is 2.0...
Text Solution
|
- A particle of mass m = 1 kg excutes SHM about mean position O with ang...
Text Solution
|
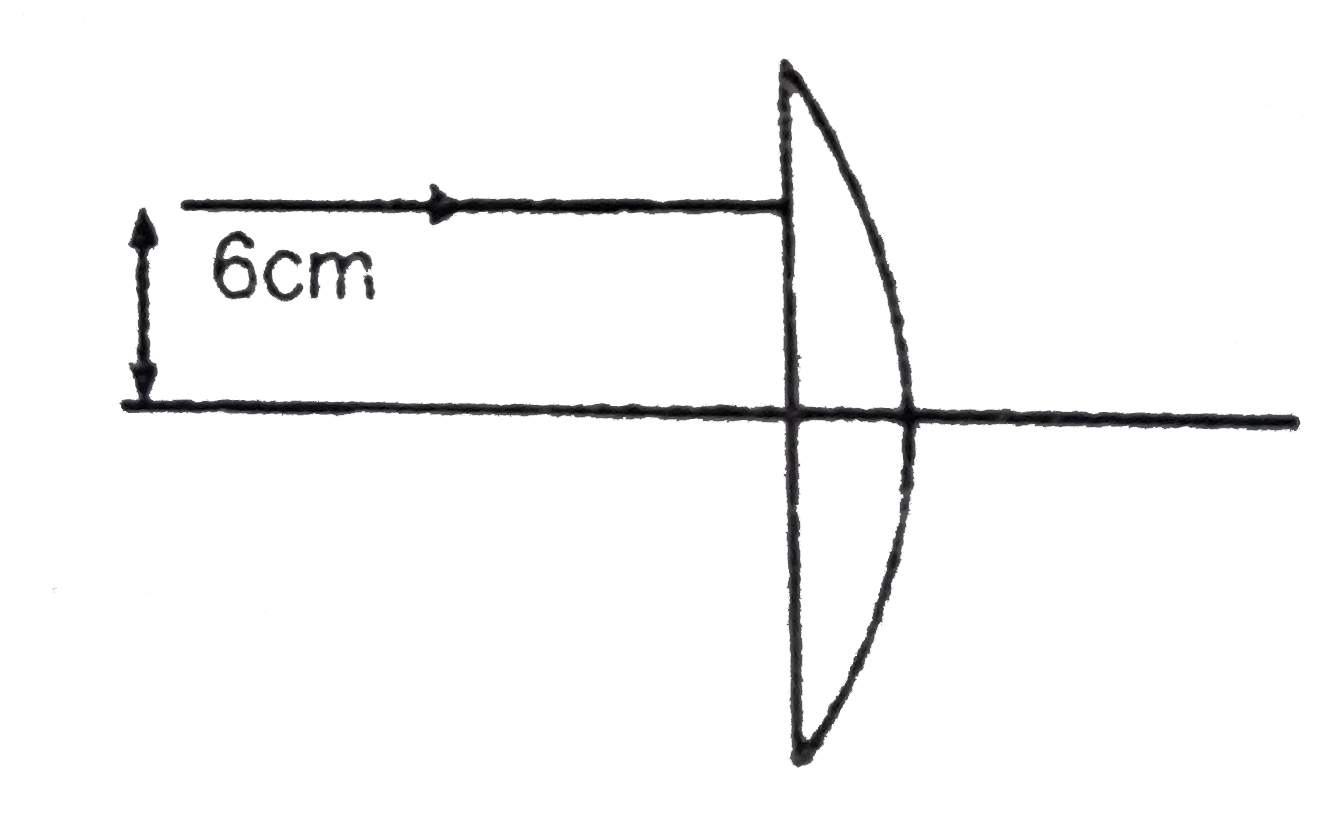
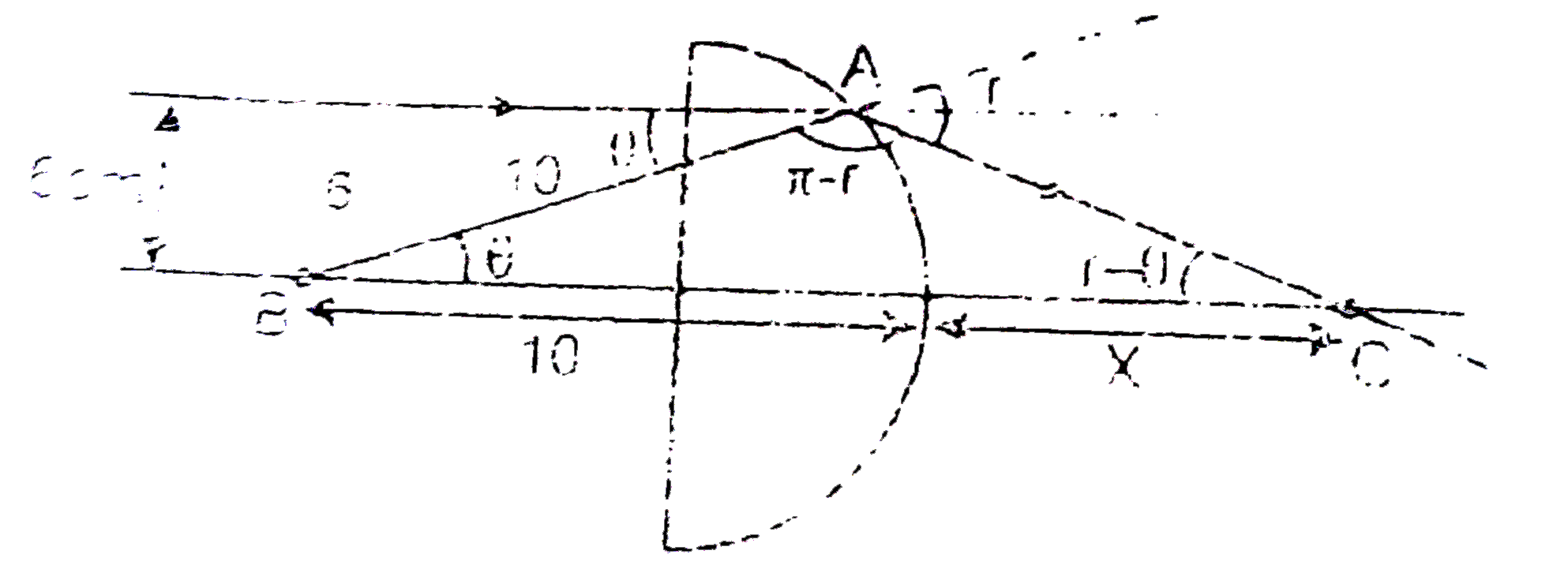
- A light ray parallel to the principal axis is incident (as shown in th...
Text Solution
|
- A small body A starts sliding from the height h down an inclined groov...
Text Solution
|
- In the decay Cu^64 rarr Ni^64 + e^+ + v, the maximum kinetic energy ...
Text Solution
|