Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DAILY PRACTICE PROBLEM
RESONANCE ENGLISH|Exercise DPP No.29|20 VideosDAILY PRACTICE PROBLEM
RESONANCE ENGLISH|Exercise DPP No.30|9 VideosDAILY PRACTICE PROBLEM
RESONANCE ENGLISH|Exercise DPP No.27|20 VideosCURRENT ELECTRICITY
RESONANCE ENGLISH|Exercise High Level Problems (HIP)|19 VideosELECTRO MAGNETIC WAVES
RESONANCE ENGLISH|Exercise Exercise 3|27 Videos
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-DAILY PRACTICE PROBLEM-DPP No.28
- A bob of mass 2kg is suspended from point O of a core with an inextens...
Text Solution
|
- Block A is kept on block B as shown in figure. It is known that accele...
Text Solution
|
- Two point charges are placed in vacuum. It is observed that electrosta...
Text Solution
|
- A 20 gm particle is subjected to two simple harmonic motions x(1)=2 ...
Text Solution
|
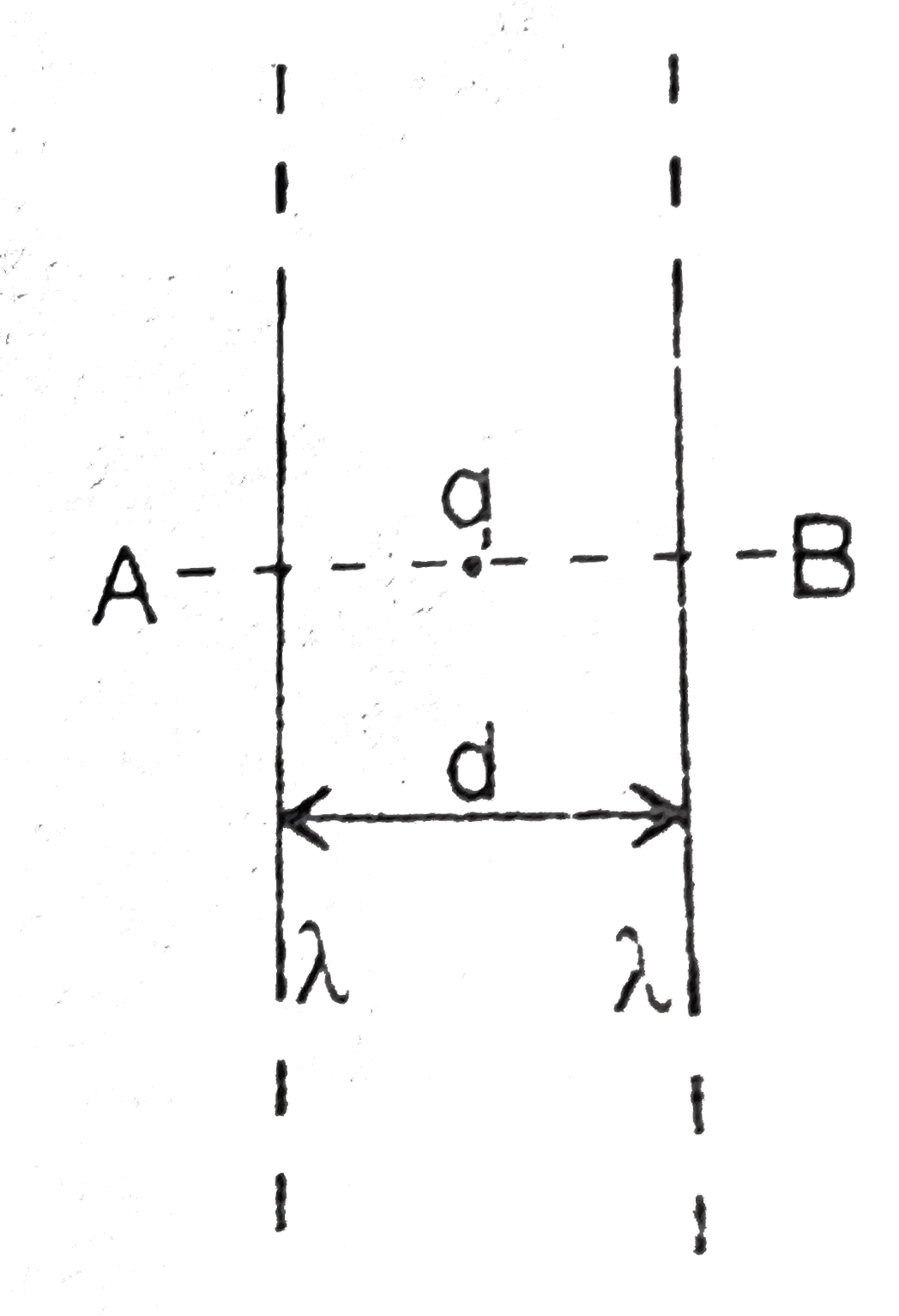
- Two infinitely long line charges having charge density lamda each are ...
Text Solution
|
- A cyclist rides along the circumference of a circular horizontal plane...
Text Solution
|
- Scientists are working hard to develop nuclear fusion reactor Nuclei o...
Text Solution
|
- Assume that two deuteron nuclei in the core of fusion reactor at tempe...
Text Solution
|
- Result of calculations for four different design of a fusion reactor u...
Text Solution
|