A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DAILY PRACTICE PROBLEM
RESONANCE ENGLISH|Exercise DPP No.31|20 VideosDAILY PRACTICE PROBLEM
RESONANCE ENGLISH|Exercise DPP No.32|9 VideosDAILY PRACTICE PROBLEM
RESONANCE ENGLISH|Exercise DPP No.29|20 VideosCURRENT ELECTRICITY
RESONANCE ENGLISH|Exercise High Level Problems (HIP)|19 VideosELECTRO MAGNETIC WAVES
RESONANCE ENGLISH|Exercise Exercise 3|27 Videos
RESONANCE ENGLISH-DAILY PRACTICE PROBLEM-DPP No.30
- X-ray from a tube with a target A of atomic number Z shows strong K(al...
Text Solution
|
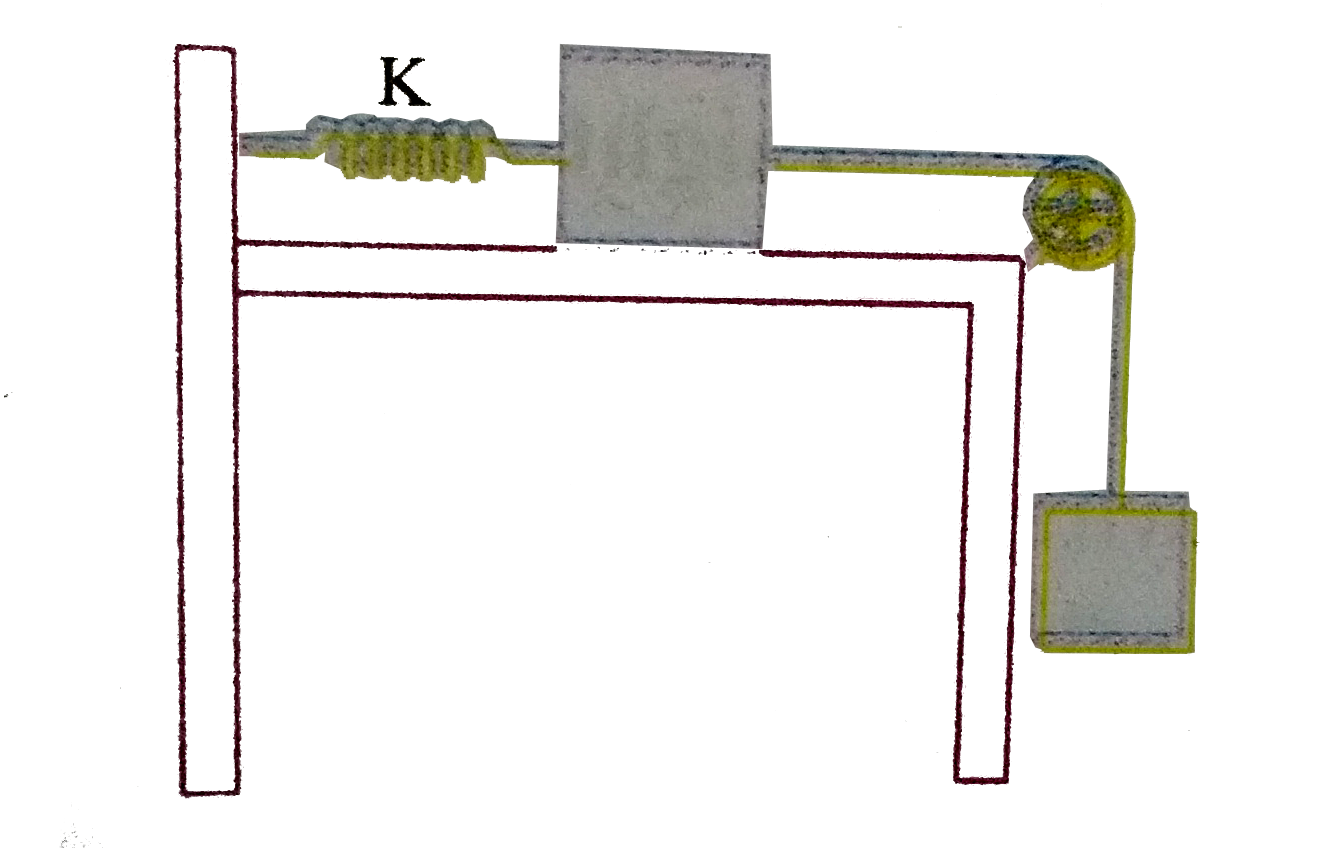
- Two blocks, of masses M and 2 M, are connected to a light spring of sp...
Text Solution
|
- A closed tube in the form of an equilateral triangle of side l contain...
Text Solution
|
- Two infinitely long rods carry equal linear denisty lambda each. They ...
Text Solution
|
- A body of mass m is thrown straight up with velocity v(0)(v(0) lt lt v...
Text Solution
|
- To activate the reaction (n, alpha) with stationary B^(11) nuclei, neu...
Text Solution
|
- Two point like charges Q(1) and Q(2) are positioned at point 1 and 2. ...
Text Solution
|
- Two point like charges Q(1) and Q(2) are positioned at point 1 and 2. ...
Text Solution
|
- Two point like charges Q(1) and Q(2) are positioned at point 1 and 2. ...
Text Solution
|
 .
.