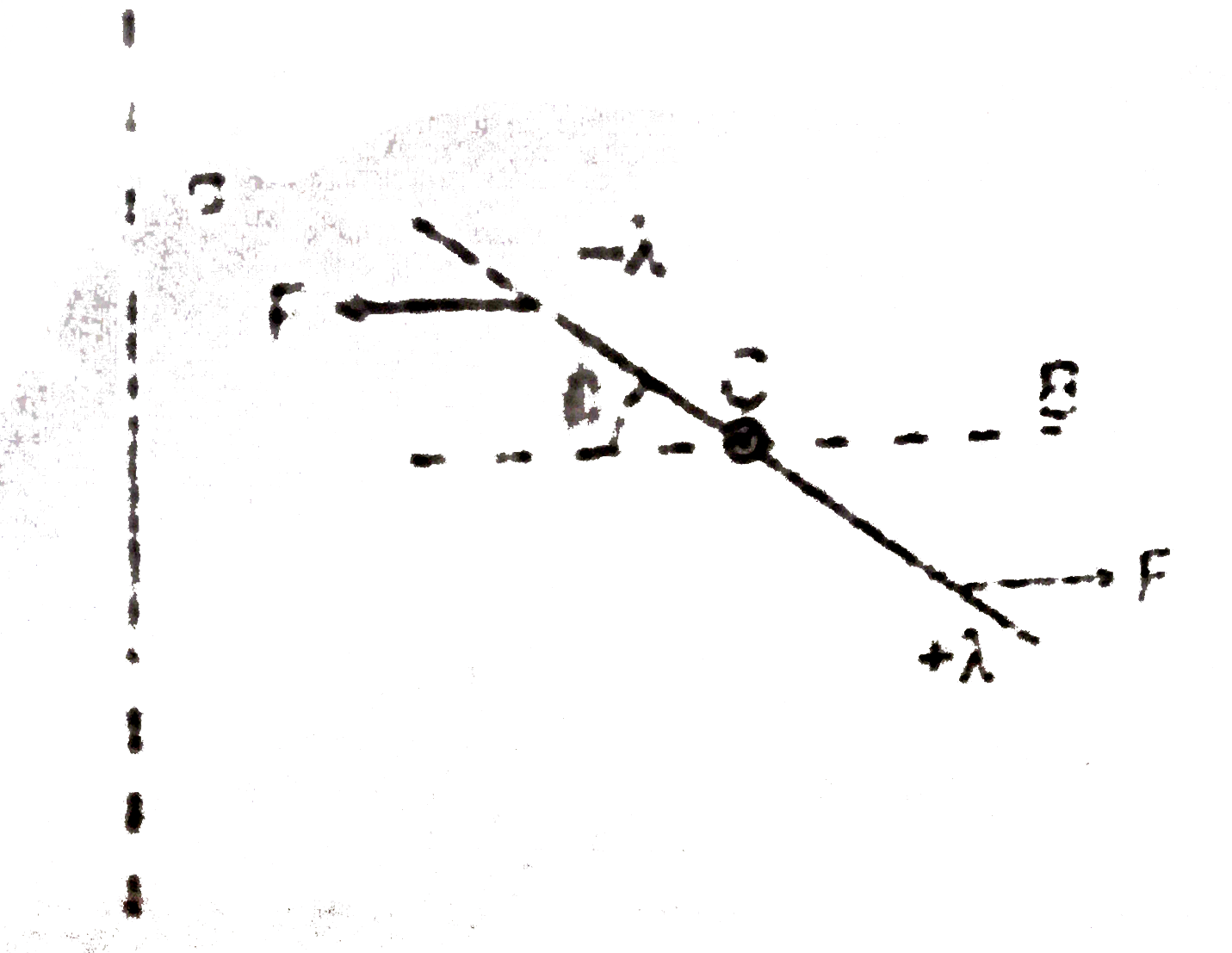Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DAILY PRACTICE PROBLEM
RESONANCE ENGLISH|Exercise DPP No.61|20 VideosDAILY PRACTICE PROBLEM
RESONANCE ENGLISH|Exercise DPP No.62|9 VideosDAILY PRACTICE PROBLEM
RESONANCE ENGLISH|Exercise DPP No.59|9 VideosCURRENT ELECTRICITY
RESONANCE ENGLISH|Exercise High Level Problems (HIP)|19 VideosELECTRO MAGNETIC WAVES
RESONANCE ENGLISH|Exercise Exercise 3|27 Videos
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-DAILY PRACTICE PROBLEM-DPP No.60
- The track shown in figure is frictionless. The block B of mass 2 m is ...
Text Solution
|
- Figure shows the path of an electron in a region of uniform magnetic f...
Text Solution
|
- A uniform rod AB of mass m and length l is hinged at its mid point C. ...
Text Solution
|
- A uniform thin rod of mass 'm' and length '3l' is released from rest f...
Text Solution
|
- A wire AB (of length 1m, area of cross section pi m^(2)) is used in po...
Text Solution
|
- A wire AB (of length 1m, area of cross section pi m^(2)) is used in po...
Text Solution
|
- A wire AB (of length 1m, area of cross section pi m^(2)) is used in po...
Text Solution
|
- A wire AB (of length 1m, area of cross section pi m^(2)) is used in po...
Text Solution
|