Home
Class 11
PHYSICS
A uniform cylinder of length L and mass ...

A uniform cylinder of length L and mass M having cross-sectional area A is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half submerged in a liquid of density `sigma` at equilibrium position. The extension `x_(0)` of the spring when it is in equilibrium is:

A

`(Mg)/(k)`

B

`(Mg)/(k)(1 - (LAsigma)/(M))`

C

`(Mg)/(k)(1 - (LAsigma)/(2M))`

D

`(Mg)/(k)(1 + (LAsigma)/(M))`

Text Solution

Verified by Experts

The correct Answer is:
C
`kx_(0) + F_(B) = mg`
`kx_(0) + sigma(L)/(2)Ag = Mg`
`x_(0) = (Mg - (sigmaLAg)/(2))/(k)`
`= (Mg)/(k)(1 - (sigmaLA)/(2M))`
Promotional Banner

Topper's Solved these Questions

  • FLUID MECHANICS

    RESONANCE ENGLISH|Exercise Advanced Level Problems|8 Videos

  • FLUID MECHANICS

    RESONANCE ENGLISH|Exercise Exercise- 3 PART - I|17 Videos

  • ELECTROSTATICS

    RESONANCE ENGLISH|Exercise Exercise|52 Videos

  • FULL TEST 1

    RESONANCE ENGLISH|Exercise Exercise|30 Videos

Similar Questions

Explore conceptually related problems

A uniform cylinder of length (L) and mass (M) having cross sectional area (A) is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half - submerged in a liquid of density (rho) at equilibrium position. When the cylinder is given a small downward push and released it starts oscillating vertically with small amplitude. If the force constant of the spring is (k) , the frequency of oscillation of the cylinder is.

A uniform cylinder of length (L) and mass (M) having cross sectional area (A) is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half - submerged in a liquid of density (rho) at equilibrium position. When the cylinder is given a small downward push and released it starts oscillating vertically with small amplitude. If the force constant of the spring is (k), the prequency of oscillation of the cylindcer is.

A uniform cylinder of length (L) and mass (M) having cross sectional area (A) is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half - submerged in a liquid of density (rho) at equilibrium position. When the cylinder is given a small downward push and released it starts oscillating vertically with small amplitude. If the force constant of the spring is (k), the prequency of oscillation of the cylindcer is.

A block of known mass is suspended from a fixed support through a ligh spring. Can you find the time period of vertical oscillation only by measuring the extension of the spring when the block is in equilibrium?

A rod of length l and mass m , pivoted at one end, is held by a spring at its mid - point and a spring at far end. The spring have spring constant k . Find the frequency of small oscillations about the equilibrium position.

A block of density 2000kg//m^3 and mass 10kg is suspended by a spring stiffness 100N//m . The other end of the spring is attached to a fixed support. The block is completely submerged in a liquid of density 1000kg//m^3 . If the block is in equilibrium position.

A cube of mass m and density D is suspended from a point P by a spring of stiffness k . The system is kept inside a beaker filled with a liquid of density d . The elongation in the spring, assuming D gt d , is :

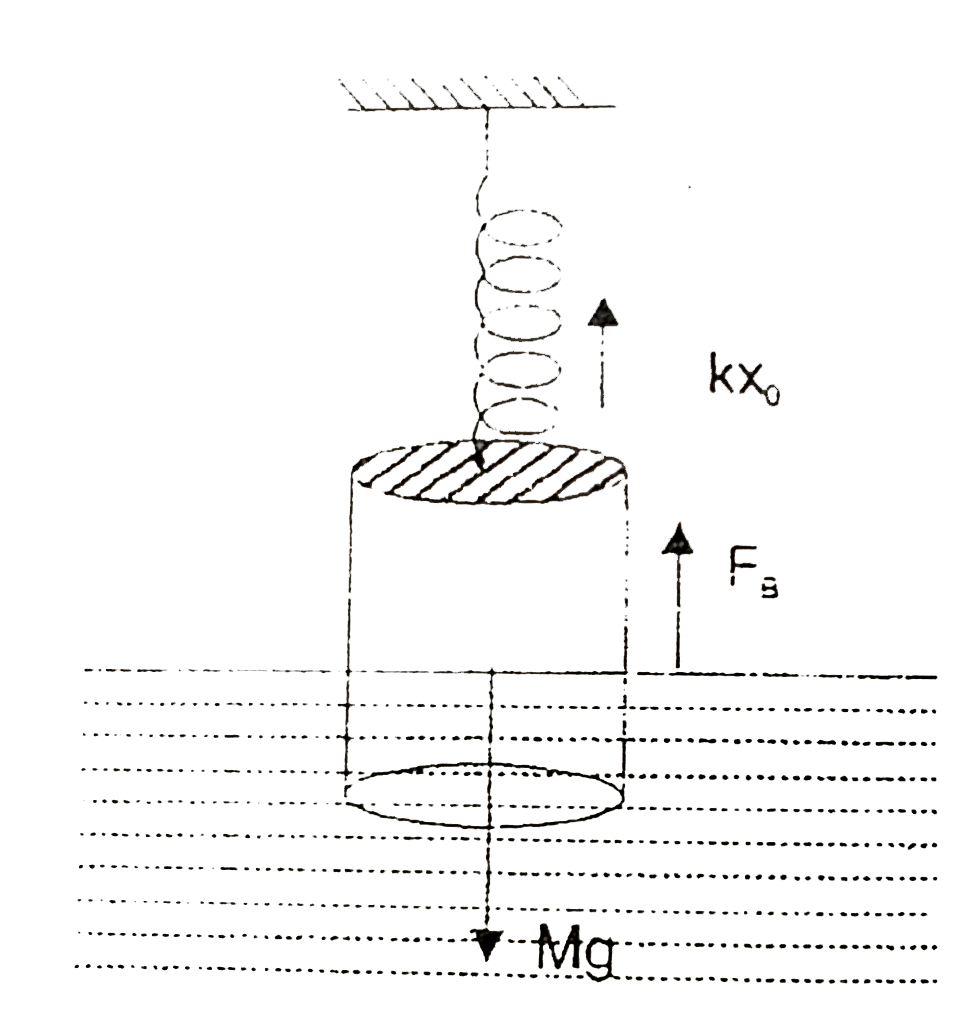
Figure shows a solid uniform cylinder of radius R and mass M , which is free to rotate about a fixed horizontal axis O and passes through centre of the cylinder. One end of an ideal spring of force constant k is fixed and the other end is higed to the cylinder at A . Distance OA is equal to (R)/(2) . An inextensible thread is wrapped round the cylinder and passes over a smooth, small pulley. A block of equal mass M and having cross sectional area A is suspended from free end of the thread. The block is partially immersed in a non-viscous liquid of density rho . If in equilibrium, spring is horizontal and line OA is vertical, calculate frequency of small oscillations of the system.

Two wires have identical lengths and areas of cross-section are suspended by mass M . Their Young's modulus are in the ratio 2:5 .

wire of length I has a ear mass density lambda and area of cross-section A and the Young's modulus y is suspended vertically from rigid support. The extension produced in wire due to its own weight