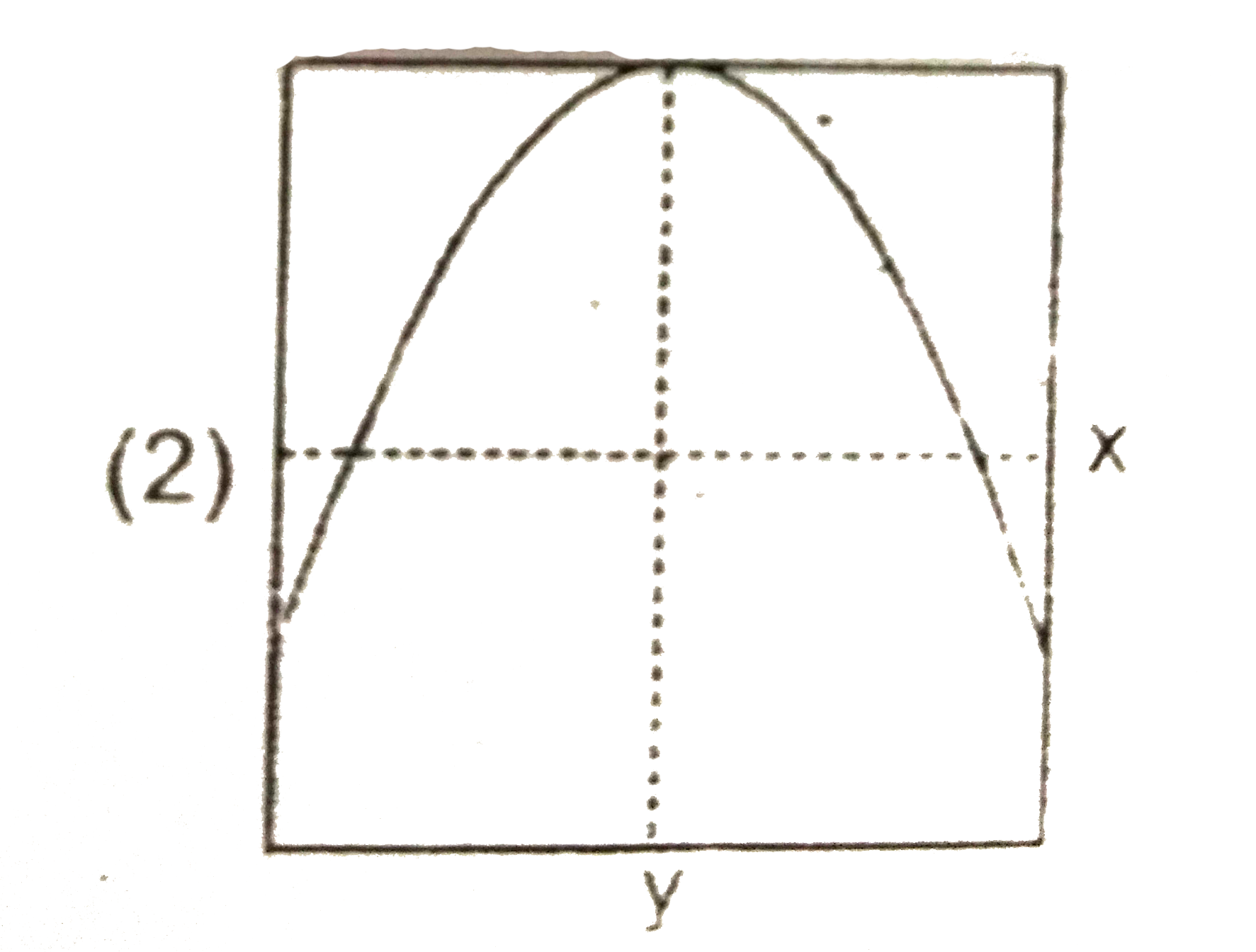
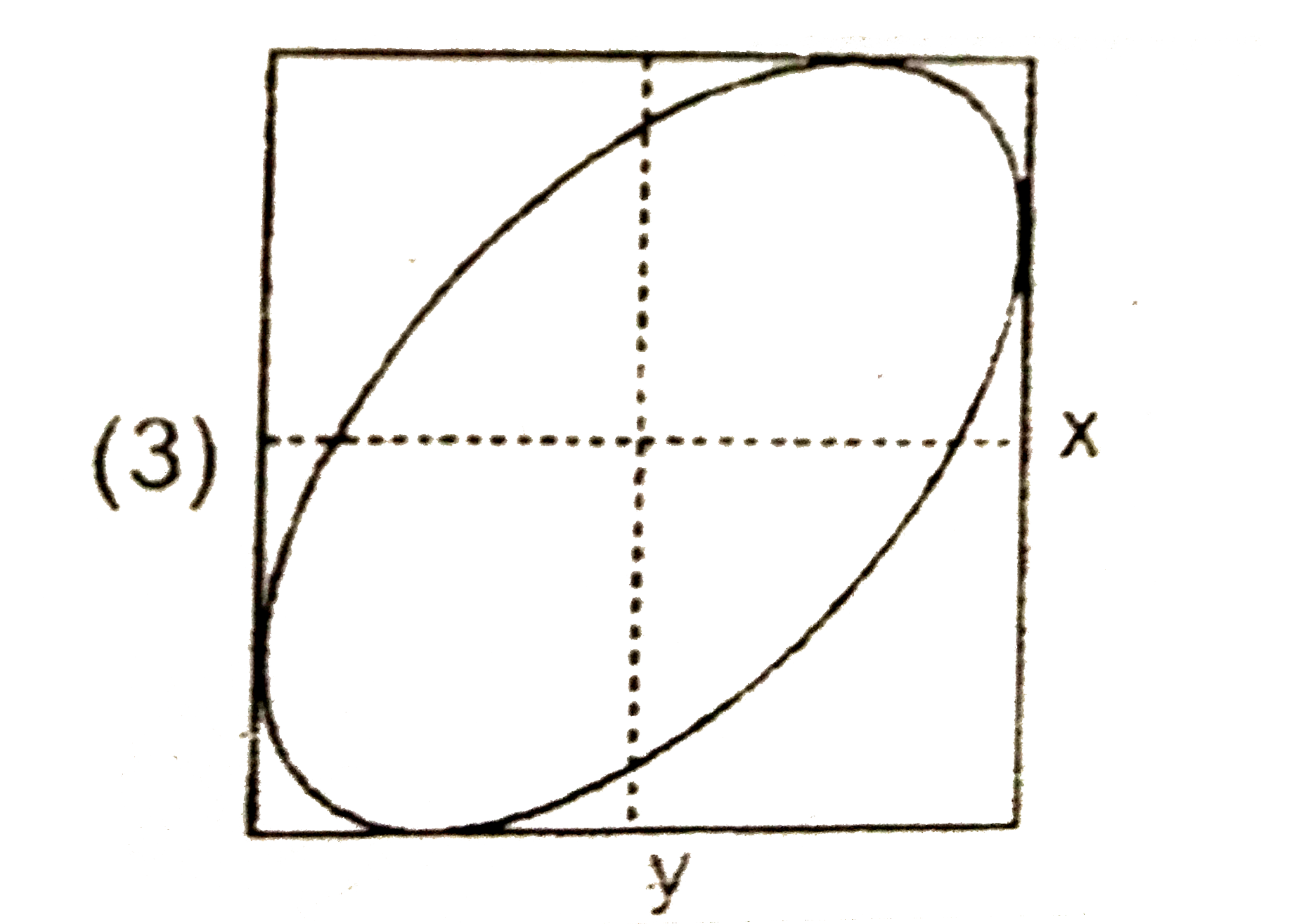
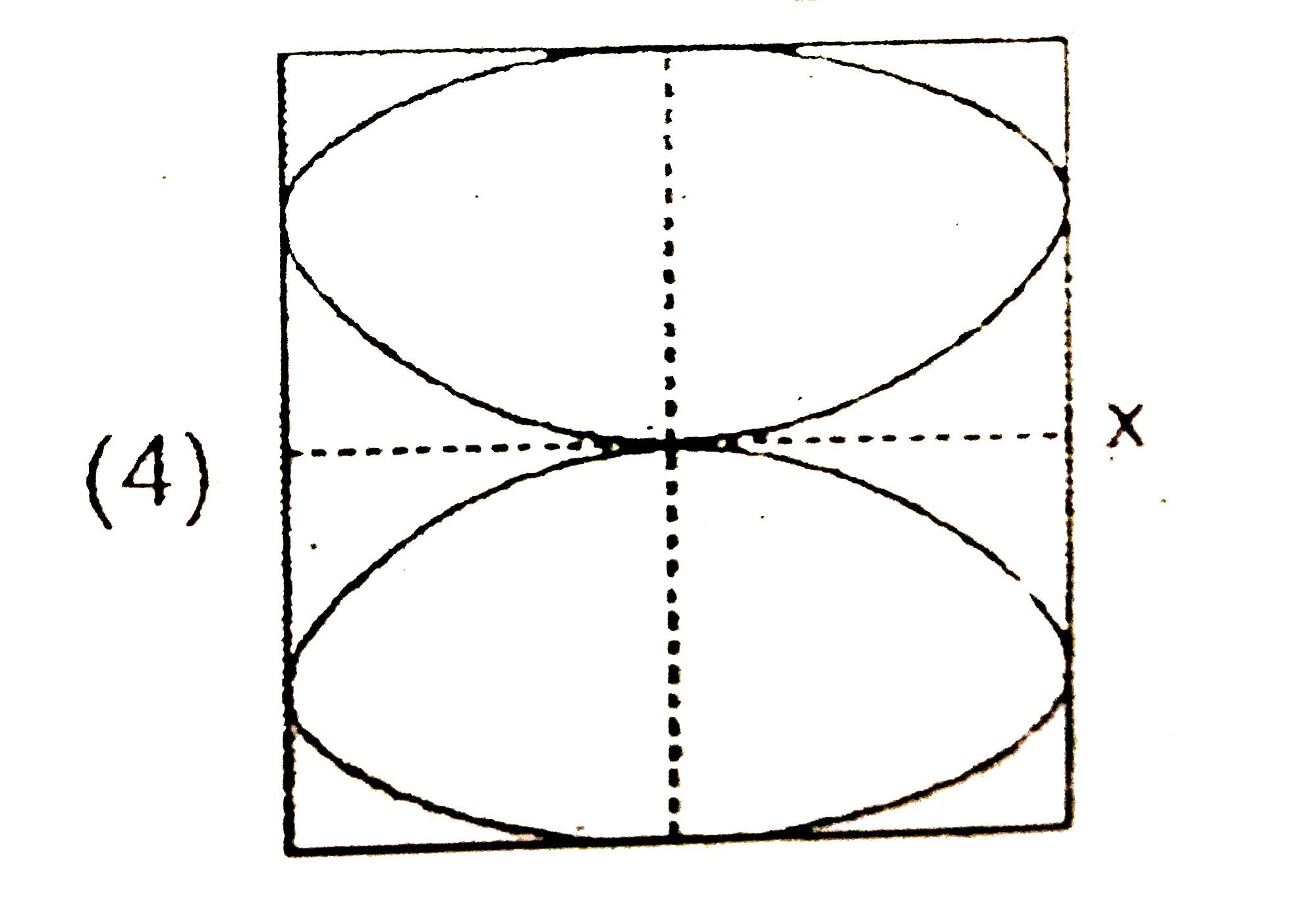
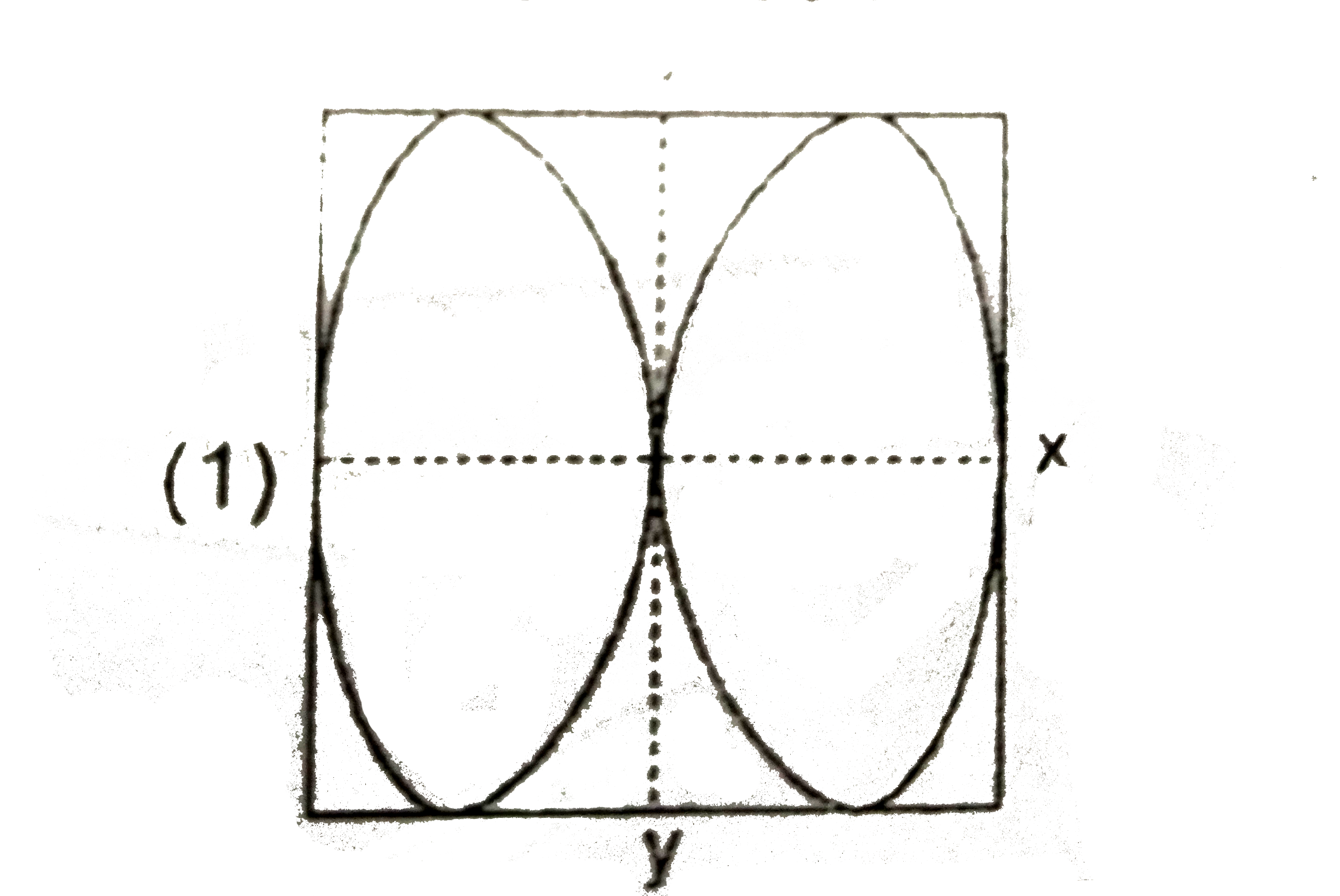A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-TEST PAPERS-PHYSICS
- In the following 'I' refers to current and other symbols have their us...
Text Solution
|
- If it takes 5 minutes to fill a 15 litre bucket from a water tap diame...
Text Solution
|
- x and y displacements of a particle are given as x(t)=-asinomegat and ...
Text Solution
|
- Suppose the drift velocity v(d) in a material varied with the applie...
Text Solution
|
- When the current in a coil changes from 5A to 2A in 0.1s, an average v...
Text Solution
|
- A 25 cm long solenoid has radius 2 cm and 500 total number of turns. I...
Text Solution
|
- You are asked to design a shaving mirror assuming that a person keeps ...
Text Solution
|
- If two glass plates have water between them and are separated by very ...
Text Solution
|
- In the circuit shown, charge on the capacitor connected between B and ...
Text Solution
|
- A 10kg weight is suspended with a wire AB of linear mass density 0.01k...
Text Solution
|
- A particle is moving in x-y plane with y=x/2 and v(x)=4-2t. The displa...
Text Solution
|
- Difference between nth and (n+1) the Bohr's radius of 'H' atom is equa...
Text Solution
|
- A radioactive substance X decays into another radioactive substance Y ...
Text Solution
|
- A charged particle enters a unifrom magnetic field with velocity vec...
Text Solution
|
- A Connot engine having an efficiency of (1)/(10) as heat engine, is u...
Text Solution
|
- A block of mass m(1) lies on the top of fixed wedge as shown in fig. a...
Text Solution
|
- A sphere of mass m and radius r is projected in a gravity free space w...
Text Solution
|
- An ideal gas undergoes a process ArarrBrarrC shown in P-V graph. Then ...
Text Solution
|
- A boy of mass 30 kg starts running from rest along a circular path of ...
Text Solution
|
- In the figure shown magnetic field B is constant and uniform and in th...
Text Solution
|