Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
SIMPLE HARMONIC MOTION
RESONANCE ENGLISH|Exercise Exercise- 1, PART - I|25 VideosSIMPLE HARMONIC MOTION
RESONANCE ENGLISH|Exercise Exercise- 1, PART - II|36 VideosSIMPLE HARMONIC MOTION
RESONANCE ENGLISH|Exercise Solved Miscellaneous Problems|9 VideosSEMICONDUCTORS
RESONANCE ENGLISH|Exercise Exercise 3|88 VideosTEST PAPERS
RESONANCE ENGLISH|Exercise PHYSICS|784 Videos
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-SIMPLE HARMONIC MOTION -Board Level Exercise
- Define amplitude of S.H.M. ?
Text Solution
|
- Why the motion of a satellite around a planet cannot be taken as S.H.M...
Text Solution
|
- Is oscillation of a mass suspended by a spring simple harmonic ?
Text Solution
|
- Which of the following examples represents (nearby) shm and which repr...
Text Solution
|
- Fill in the blanks using appropriate word from the list at the end of ...
Text Solution
|
- A restoring force is a must for a body to execute S.H.M Explain, why
Text Solution
|
- A man is standing on a platform moving up and down as a S.H.M. will th...
Text Solution
|
- An air chamber of volume V has a neck area of cross section A into whi...
Text Solution
|
- Show that for a particle in linear SHM the average kinetic energy over...
Text Solution
|
- A man with a wrist watch on his hand falls from the top of a tower. Do...
Text Solution
|
- Time period of a particle in shm depends on the force constant k and m...
Text Solution
|
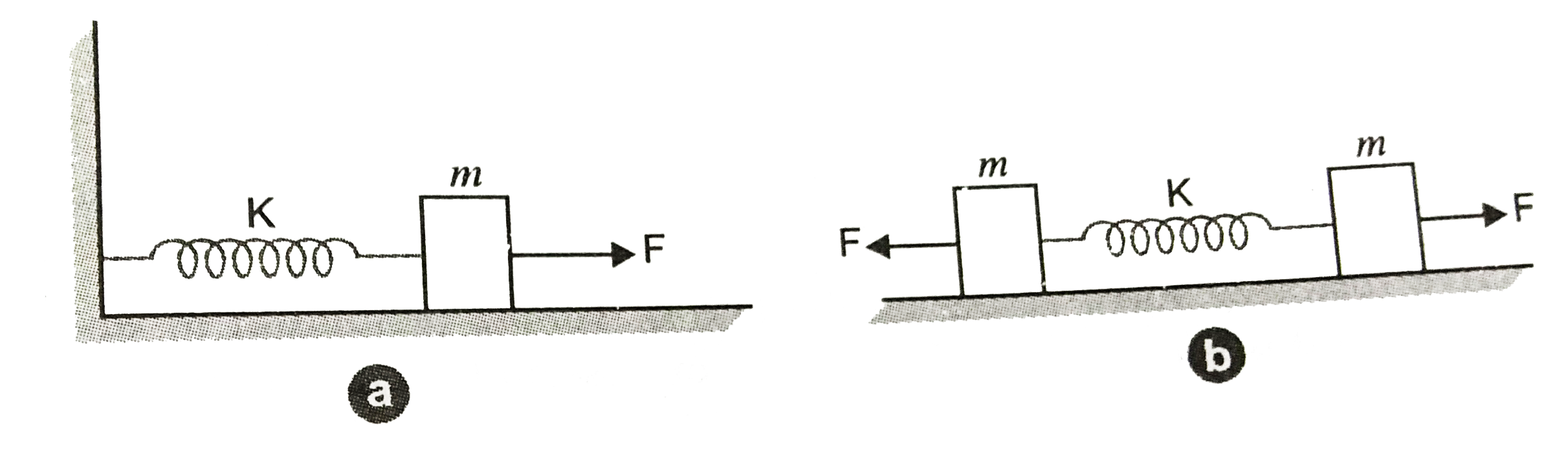
- Figure a) shows a spring of force constant k clamped rigidly at once e...
Text Solution
|
- (a) Define simple harmonic motion and derive, an expression for the pe...
Text Solution
|
- Answer the following question What is the inverse of frequency of osc...
Text Solution
|
- A simple pendulum of length L and having a bob of mass m is suspended ...
Text Solution
|
- Define resonance and resonance energy. What are the conditions for res...
Text Solution
|
- Explain damped harmonic oscillation and the equation of such oscillati...
Text Solution
|
- Explain damped harmonic oscillation and the equation of such oscillati...
Text Solution
|
- Write the expression for equivalent spring constant of (i) parallel ...
Text Solution
|
- Find equivalent spring constant for the system:
Text Solution
|