(R) is:

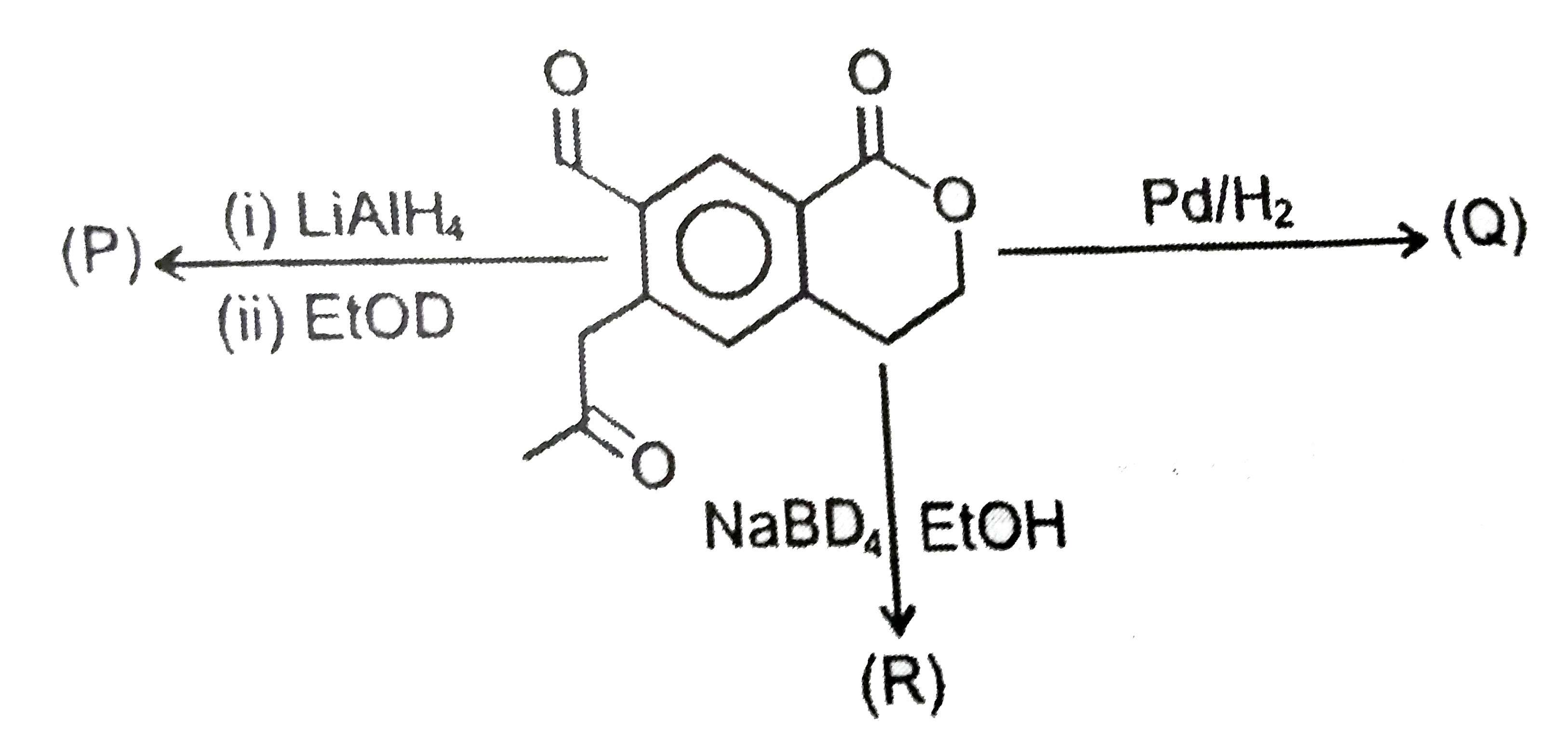
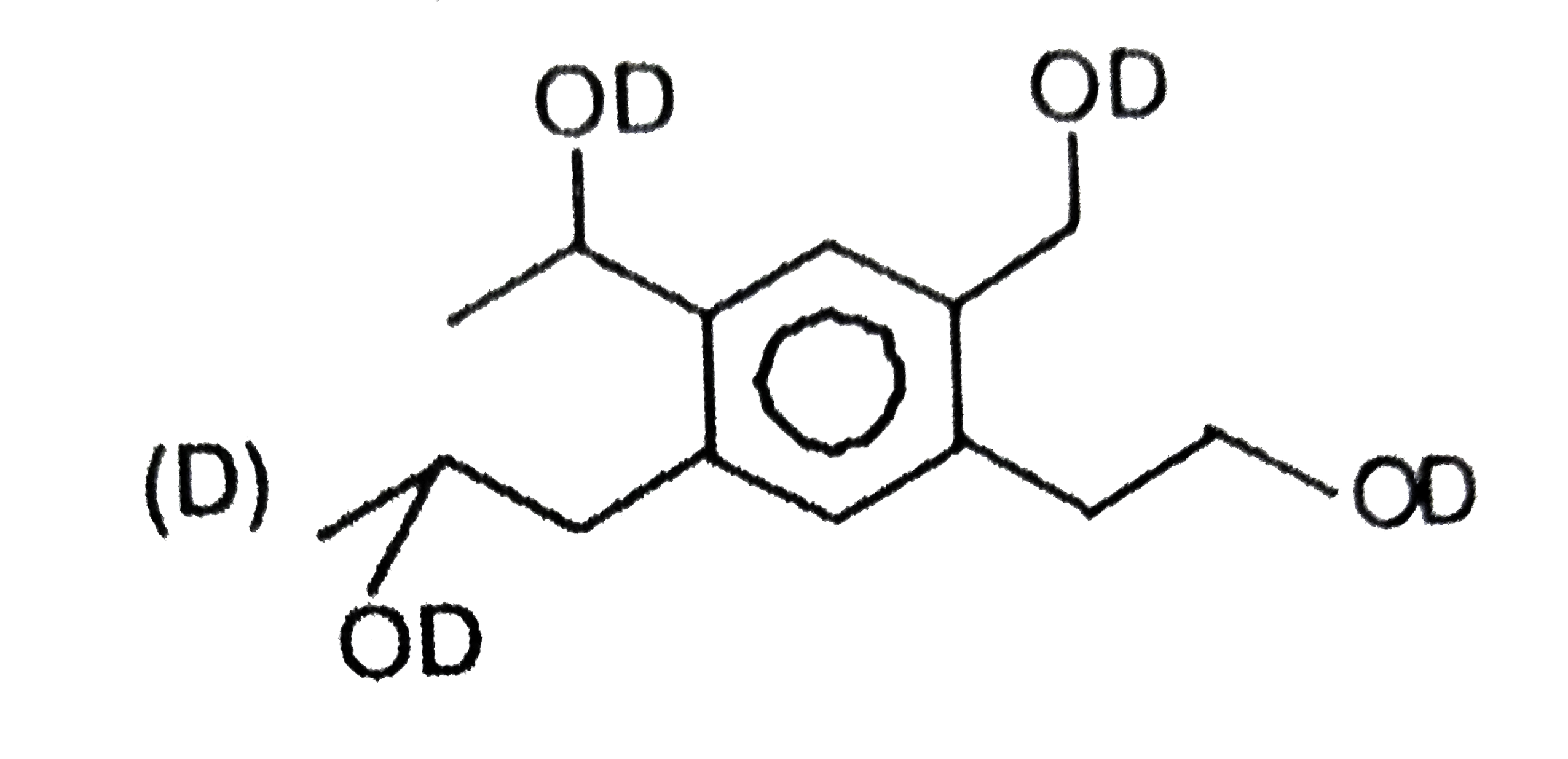
A

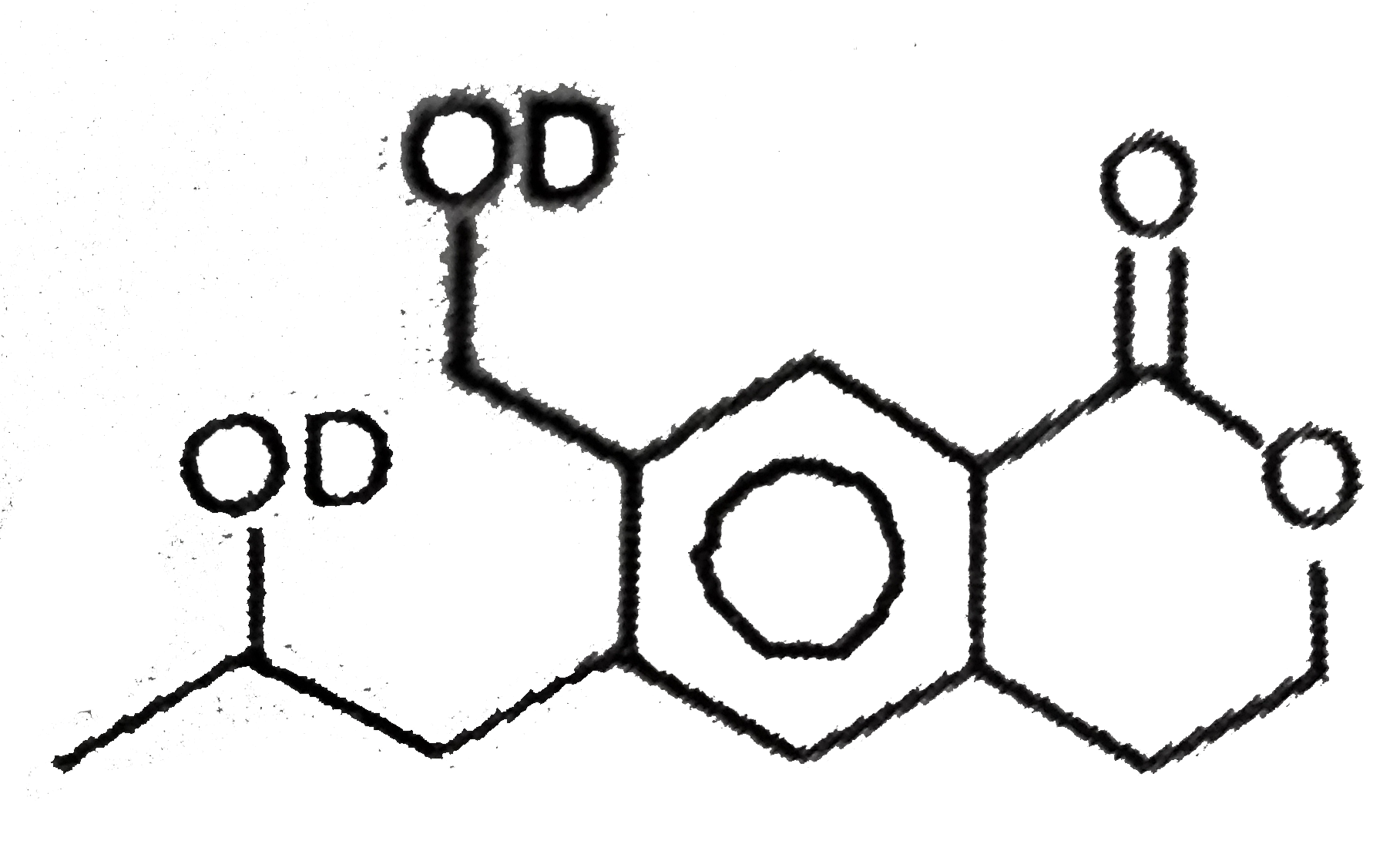
B

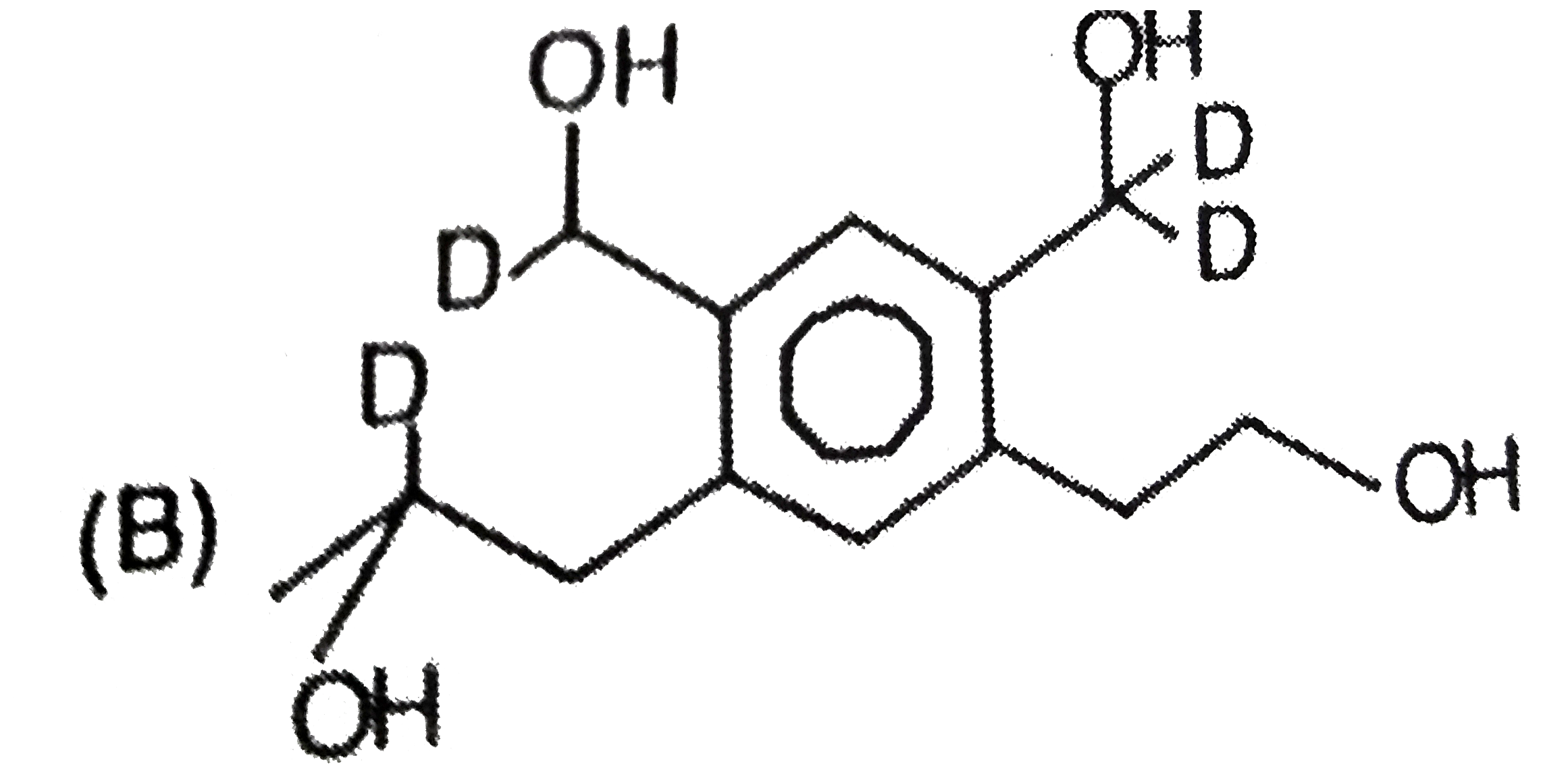
C

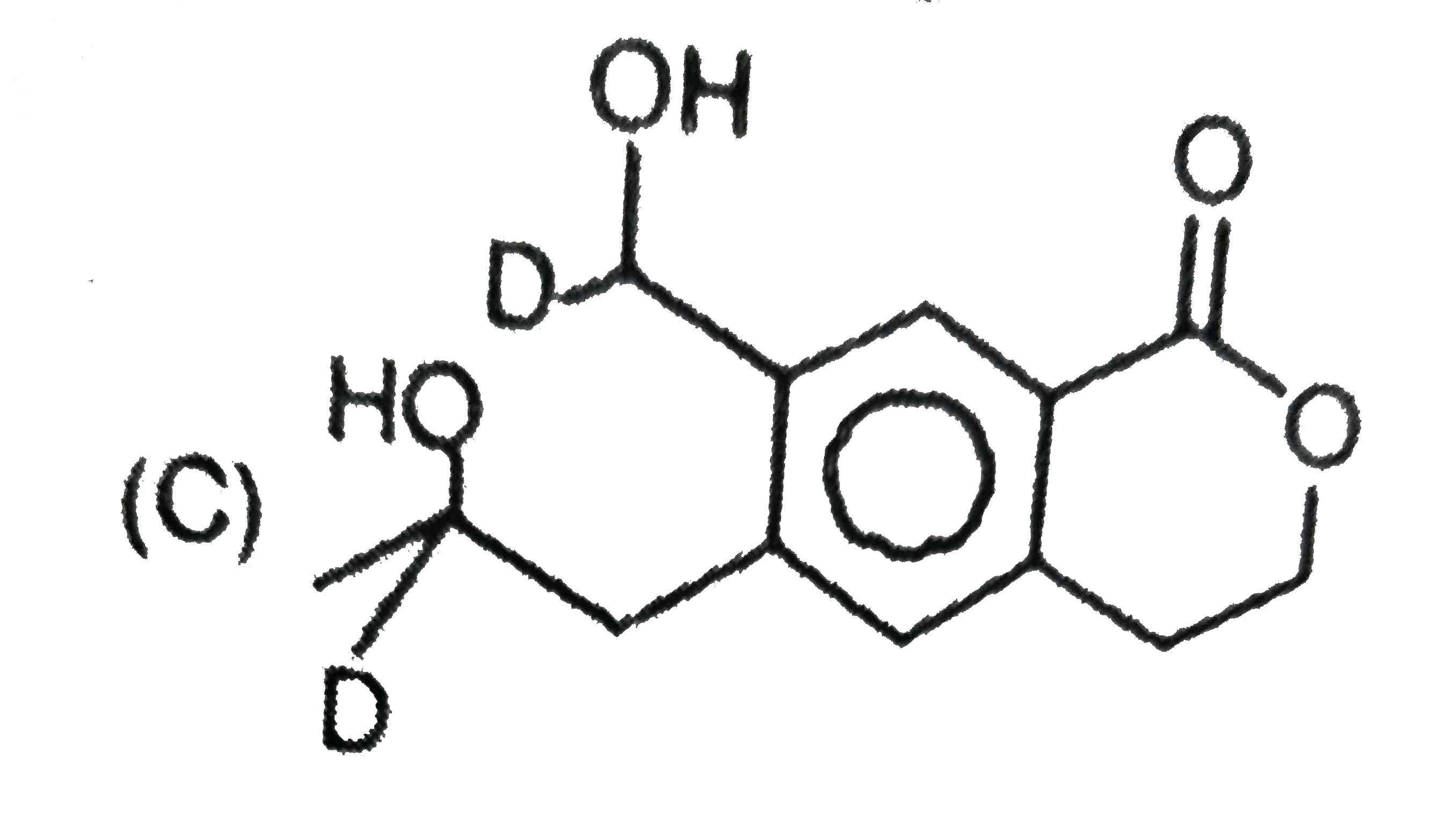
D

Text Solution

Verified by Experts

The correct Answer is:
C
Promotional Banner

Topper's Solved these Questions

  • REDUCTION, OXIDATION & HYDROLYSIS REACTIONS

    RESONANCE ENGLISH|Exercise Part-I : Jee (Advanced) (Previous years)|12 Videos

  • REDUCTION, OXIDATION & HYDROLYSIS REACTIONS

    RESONANCE ENGLISH|Exercise Part-II JEE (Main) AIEEE Problems (Previous Years)|16 Videos

  • REDUCTION, OXIDATION & HYDROLYSIS REACTIONS

    RESONANCE ENGLISH|Exercise Part-III: One or more than one options correct type|4 Videos

  • PERIODIC TABLE & PERIODICITY

    RESONANCE ENGLISH|Exercise ORGANIC CHEMISTRY(BASIC CONCEPTS)|27 Videos

  • S BLOCK ELEMENTS

    RESONANCE ENGLISH|Exercise ORGANIC CHEMISTRY(Biomolecules & Polymer)|4 Videos

Similar Questions

Explore conceptually related problems

Two resistance R_(1) and R_(2) are made of different material. The temperature coefficient of the material of R_(1) is alpha and of the material of R_(2) is -beta . Then resistance of the series combination of R_(1) and R_(2) will not change with temperature, if R_(1)//R_(2) will not change with temperature if R_(1)//R_(2) equals

Two resistance R_(1) and R_(2) are made of different material. The temperature coefficient of the material of R_(1) is alpha and of the material of R_(2) is -beta . Then resistance of the series combination of R_(1) and R_(2) will not change with temperature, if R_(1)//R_(2) will not change with temperature if R_(1)//R_(2) equals

Two resistors of resistances R_(1)=100 pm 3 ohm and R_(2)=200 pm 4 ohm are connected (a) in series, (b) in parallel. Find the equivalent resistance of the (a) series combination, (b) parallel combination. Use for (a) the relation R=R_(1)+R_(2) and for (b) 1/(R')=1/R_(1)+1/R_(2) and (Delta R')/R'^(2)=(Delta R_(1))/R_(1)^(2)+(Delta R_(2))/R_(2)^(2)

Find r if (i) ""^5P_r=2^6P_(r-1) (ii) ""^5P_r=^6P_(r-1)

Show that + : R xx R ->R and xx : R xx R ->R are commutative binary operations, but - : RxxR ->R and -: : R_ *xxR_* ->R_* are not commutative.

cosA+cosB+cosC is equal to (A) r/R (B) R/r (C) 1 (D) 1+r/R

If r,r_(1) ,r_(2), r_(3) have their usual meanings , the value of 1/(r_(1))+1/(r_(2))+1/(r_(3)) , is

Let there be a spherical symmetric charge density varying as p(r )=p_(0)(r )/(R ) upto r = R and rho(r )=0 for r gt R , where r is the distance from the origin. The electric field at on a distance r(r lt R) from the origin is given by -

Prove that 2R cos A = 2R + r - r_(1)

The circles having radii r_1a n dr_2 intersect orthogonally. The length of their common chord is (2r_1r_2)/(sqrt(r1^2+r2^2)) (b) (sqrt(r1^2+r2^2))/(2r_1r_2) (r_1r_2)/(sqrt(r1^2+r1^2)) (d) (sqrt(r1^2+r1^2))/(r_1r_2)