Text Solution
Verified by Experts
Topper's Solved these Questions
GRAVITATION
RESONANCE ENGLISH|Exercise EXAMPLE|2 VideosGRAVITATION
RESONANCE ENGLISH|Exercise EXERCISE-1 PART-1|9 VideosGRAVITATION
RESONANCE ENGLISH|Exercise HIGH LEVEL PROBLEMS|16 VideosGEOMATRICAL OPTICS
RESONANCE ENGLISH|Exercise Advance level Problems|35 VideosNUCLEAR PHYSICS
RESONANCE ENGLISH|Exercise Advanced level solutions|16 Videos
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-GRAVITATION-SOLVED MISCELLANEOUS PROBLEMS
- Calculate the force exerted by point mass m on rod of uniformly distri...
Text Solution
|
- Three particle each of mass m, are located at the vertices of an equil...
Text Solution
|
- In a double star, two stars one of mass m(1) and another of mass m(2),...
Text Solution
|
- For a particle projected in a transverse direction from a height h abo...
Text Solution
|
- A rocket starts vertically upward with speed v(0). Show that its speed...
Text Solution
|
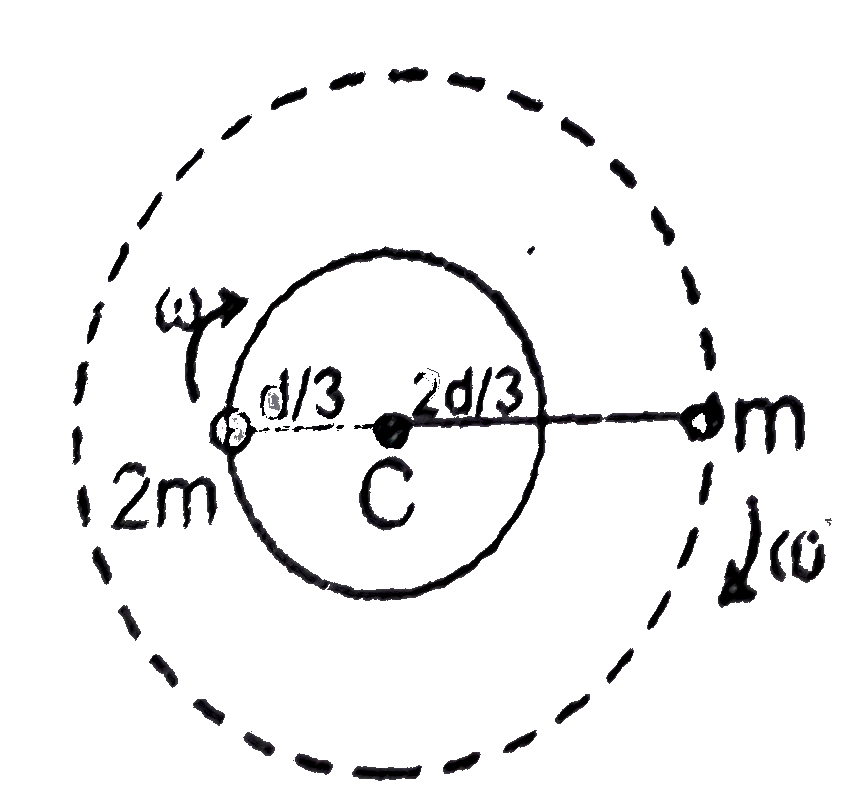 .
.