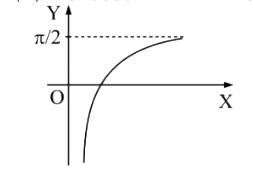
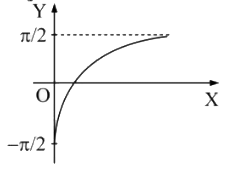
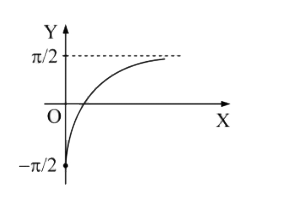
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
DIFFERENTIAL CALCULUS 2
VMC MODULES ENGLISH|Exercise Numerical ValueType for JEE Main|14 VideosDIFFERENTIAL CALCULUS 2
VMC MODULES ENGLISH|Exercise JEE Main (Archive)|36 VideosDIFFERENTIAL CALCULUS 2
VMC MODULES ENGLISH|Exercise Level -1|102 VideosDIFFERENTIAL CALCULUS
VMC MODULES ENGLISH|Exercise JEE Advanced (Archive)|75 VideosDIFFERENTIAL EQUATIONS
VMC MODULES ENGLISH|Exercise JEE ADVANCE (ARCHIVE )|32 Videos
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-DIFFERENTIAL CALCULUS 2-Level -2
- Let f(x) be a non-constant twice differentiable function defined on (-...
Text Solution
|
- f: (0,oo) to (-pi/2,pi/2)" be defined as, "f(x)=tan^(-1) (log(e)x). ...
Text Solution
|
- f: (0,oo) to (-pi/2,pi/2)" be defined as, "f(x)=tan^(-1) (log(e)x). ...
Text Solution
|
- f: (0,oo) to (-pi/2,pi/2)" be defined as, "f(x)=tan^(-1) (log(e)x). ...
Text Solution
|
- Given a function f:[0,4]toR is differentiable ,then prove that for som...
Text Solution
|
- With the help of Lagrange's formula, prove that (a-b)/(a) le log (a/b)...
Text Solution
|
- The function f(x)=int(0)^(x)sqrt(1-t^(4)) dt is such that
Text Solution
|
- The function (sin(x+a))/(sin(x+b)) has no maxima or minima if
Text Solution
|
- The set of value(s) of a for which the function f(x)=(a x^3)/3+(a+2)x^...
Text Solution
|
- If f(x) is a cubic polynomial which has local maximum at x=-1,If f(2...
Text Solution
|
- If f(x) is a polynomial of degree 4 having extremum at x=1,2 and lim(x...
Text Solution
|
- The maximum value of the function f(x)=3x^(3)-18x^(2)+27x-40 on the s...
Text Solution
|
- If the function f(x)=x^(4)+bx^(2)+8x+1 has a horizontal tangent and a...
Text Solution
|
- Let p(x) be a real polynomial of least degree which has a local maximu...
Text Solution
|
- The equation x^3-3x+[a]=0, where [*] denotes the greatest integer func...
Text Solution
|
- If the function f:[0,4]vecR is differentiable, the show that for a , b...
Text Solution
|
- For a twice differentiable function f(x),g(x) is defined as g(x)=f^(pr...
Text Solution
|
- A function y=f(x) has a second-order derivative f''(x)=6(x-1)dot It it...
Text Solution
|
- Function f(x), g(x) are defined on [-1, 3] and f''(x) > 0, g''(x) > 0 ...
Text Solution
|
- If a << b << c << d and x in R then the least value of the function,...
Text Solution
|