Home
Class 12
PHYSICS
A transverse hormonic wave on a string o...

A transverse hormonic wave on a string on a string is descibed by
`y(x,t)=3.0sin(36t+0.018x+(pi)/(4))`
Where x and y are in cm and t is in sec. The positve direction of x is from left to rigth .

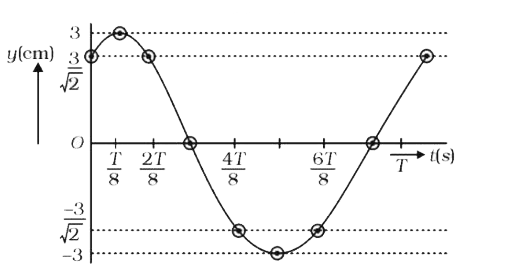
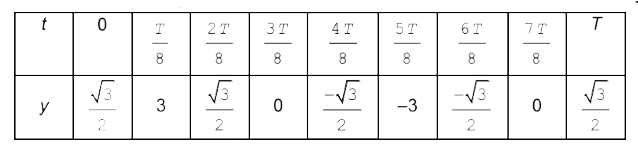
Text Solution

Verified by Experts

The transverse harmonic wave is `y(x,t)=3.0sin[36t+0.018x+(pi)/(4)]`
for x=0,
`y(0,t)=3.0sin(36t+pi//4)`
Here, `omega=(2pi)/(T)=36,T=(2pi)/(36)=(pi)/(18)s`

For different values of t, we calculate y using equation (i). These values are tabulated below : On plotting y versus t graph, we obtained a sinusoidal curve as shown in above figure.

Similar are obtained for x=2 cm and x=4 cm.
The oscillatory motion in travelling wave differs from one point to another only in terms of phase. Amplitude and frequency of oscillatory motion remain the same in all the three cases
Promotional Banner

Topper's Solved these Questions

  • WAVE MOTION

    VMC MODULES ENGLISH|Exercise LEVEL-1|75 Videos

  • WAVE MOTION

    VMC MODULES ENGLISH|Exercise LEVEL-2|41 Videos

  • UNITS, MEASUREMENTS & ERRORS

    VMC MODULES ENGLISH|Exercise IN - CHAPTER EXERCISE - B|10 Videos

  • WORK ENERGY AND POWER

    VMC MODULES ENGLISH|Exercise IMPECCABLE|54 Videos

Similar Questions

Explore conceptually related problems

A transverse harmonic wave on a string is described by y(x,t)=3.0sin(36t+0.018x+pi//4) where x, y are in cm, t in second. The positive direction of x is from left to right . (i) Is this a travelling or stationary wave ? If travellying, what are the speed and direction of its propagation ? (ii) what are its amplitude and frequency ? (iii) what is the inital phase at the origing ? (iv) What is the least distance between two successive creests in the wave?

A transverse harmonic wave on a string is described by y(x, t) = 3sin ( 36t + 0.018x + π/4) where x and Y are in cm and t is in s. Which of the following statements is incorrect?

A transverse wave propagating along x-axis is represented by: y(x,t)=8.0sin(0.5pix-4pit-(pi)/(4)) Where x is in metres and t is in seconds. The speed of the wave is:

The linear density of a vibrating string is 10^(-4) kg//m . A transverse wave is propagating on the string, which is described by the equation y=0.02 sin (x+30t) , where x and y are in metres and time t in seconds. Then tension in the string is

A transverse wave along a string is given by y = 2 sin (2pi (3t - x) + (pi)/(4)) where x and y are in cm and t in second. Find acceleration of a particle located at x = 4 cm at t = 1s.

The linear density of a vibrating string is 1.3 xx 10^(-4) kg//m A transverse wave is propagating on the string and is described by the equation y= 0.021 sin (x + 30 t) where x and y are measured in meter and t t in second the tension in the string is :-

The equation of a transverse wave is given by y=10 sin pi (0.01 x -2t ) where x and y are in cm and t is in second. Its frequency is

A transverse wave travelling on a taut string is represented by: Y=0.01 sin 2 pi(10t-x) Y and x are in meters and t in seconds. Then,

A transverse wave propagating along x-axis is represented as y(x,t)= 0.8sin(pi/4-4pit-pi/2x) where x is in meter and t is in second. The velocity of wave is

A transversee wave propagating on the string can be described by the equation y= 2 sin (10 x + 300 t) , where x and y are in metres and t in second. If the vibrating string has linear density of 0.6 xx 10^(-3) g//cm , then the tension in the string is