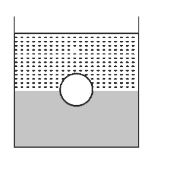
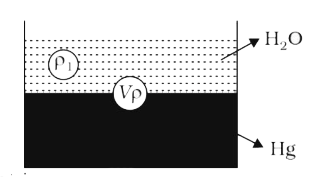
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
LIQUIDS
VMC MODULES ENGLISH|Exercise LEVEL -2|50 VideosLIQUIDS
VMC MODULES ENGLISH|Exercise JEE MAIN (LEVEL - 1 )|31 VideosLIQUIDS
VMC MODULES ENGLISH|Exercise LEVEL-0 ( Short Answer Type - II )|15 VideosLAWS OF MOTION
VMC MODULES ENGLISH|Exercise IMPECCABLE|53 VideosMAGNETIC EFFECTS OF CURRENT
VMC MODULES ENGLISH|Exercise JEE Advanced (Archive)|78 Videos
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-LIQUIDS-LEVEL -1
- A container is partially filled with a liquid of density rho2 A capill...
Text Solution
|
- A drop of liquid of density rho is floating half-immersed in a liquid ...
Text Solution
|
- A large open top container of negligible mass and uniform cross sectio...
Text Solution
|
- A liquid flows through two capillary tubes A and B connected in series...
Text Solution
|
- A uniform tube is shown in figure, Which is open at one en and closed ...
Text Solution
|
- If a 5.0 cm long capillary tube with 0.10 mm internal diameter open at...
Text Solution
|
- A cubical block (of sie 2m) of mass 20 kg slides on inclined plane lub...
Text Solution
|
- A drop of water of radius 0.0015 mm is falling in air. If the coeffici...
Text Solution
|
- A metallic sphere of radius 1.0 xx 10^(-3) m and density 1.0 xx 10^(4)...
Text Solution
|
- The cylindrical tube of a spray pump has a cross-section of 8 cm^2, on...
Text Solution
|
- An iceberg is floating in water. The density of ice in the iceberg is ...
Text Solution
|
- A mercury drop of radius 1.0 cm is sprayed into 10^(6) droplets of equ...
Text Solution
|
- The excess pressure inside a spherical drop of water is four times tha...
Text Solution
|
- Work done in forming a liquid drop of radius R is W(1) and that of rad...
Text Solution
|
- The surface tension of a liquid is 5 Newton per metre. If a film is he...
Text Solution
|
- Two liquids of densities 2 rho " and " rho having their volumes in the...
Text Solution
|
- A container (see figure) contains a liquid upto a height h. The densit...
Text Solution
|
- A film of soap solution is formed on a loop frame loop of 6.28 cm long...
Text Solution
|
- Eight spherical rain drops of the same mass and radius are falling dow...
Text Solution
|
- A solid uniform ball of volume V floats on the interface of two immisc...
Text Solution
|