Home
Class 12
PHYSICS
A bar of cross-section A is subjected to...

A bar of cross-section A is subjected to equal and opposite tensile forces at its ends. Consider a plane section of the bar whose normal makes an angle `theta` with the axis of the bar .
(i) What is the tensile stress on this plane?
(ii) What is the shearing stress on this plane?
(iii) For what value of `theta` is the tensile stress maximum
(iv) For what value of `theta` is the shearing stress maximum?

Text Solution

Verified by Experts

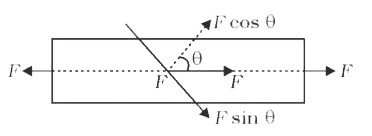
(i) The resolved part of F along the normal is the tensile force on this plane and the resolved part parallel to the plane is the shearing force on the plane.
`therefore` Area of plane section `=Asectheta`
Tensile stress `=("Force")/("Area")=(F costheta)/(Asectheta)" " =(F)/(A)cos^(2)theta`
(ii) Shearing stress applied on the plane
So , `F=Fsintheta`
Shearing stress `=("Force")/("Area")=(Fsintheta)/(Asectheta)=(F)/(A)sin thetacostheta`
`=(F)/(2A)sin2theta " " [becausesin2theta=2sinthetacostheta]`
(iii) Tensile stress will be maximum when `cos^(2)theta` is maximum i.e., `costheta=1 or theta=0^(@)` (iv) Shearing stress will be maximum when `sin2theta` is maximum i.e . `sin2theta=1` or `2theta=90^(@)ortheta=45^(@)` .
Promotional Banner

Topper's Solved these Questions

  • PROPERTIES OF MATTER

    VMC MODULES ENGLISH|Exercise Level -1|90 Videos

  • PROPERTIES OF MATTER

    VMC MODULES ENGLISH|Exercise Level -2|50 Videos

  • MOVING CHARGES & MAGNETISM

    VMC MODULES ENGLISH|Exercise IN-CHAPTER EXERCISE-K|10 Videos

  • QUIZ

    VMC MODULES ENGLISH|Exercise PHYSICS|30 Videos

Similar Questions

Explore conceptually related problems

A bar of cross section A is subjected to equal and opposite tensile force at its ends. Consider a plane section of the bar whose normal makes an angle theta with the axis of the bar. a. What is the tensile stress on the plane? b. What is the shearing stress on the this plane? c. For what value of theta is the tensile stress maximum? d. For what value of theta is the shearing stress maximum?

A bar of cross-section A is subjected two equal and opposite tensile forces at its ends consider a plane section of the bar whose makes an angle theta with the axis of the bar. (a) what is the tensile stress on this plane ? (b)what is the shearing stress on this plane ? (c )for what value of theta is the tensile stress is maximum ? (d) for what value of theta is the shearing stress maximum ?

A bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle theta with a plane at right angles to the bar as shown in figure. The tensile stress at this plane in terms of F, A and theta is

A bar of cross- sectional area A is is subjected two equal and opposite tensile forces at its ends as shown in figure. Consider a plane BB' making an angle theta with length. The ratio of tensile stress to the shearing stress on the plane BB' is

Consider a long steel bar under a tensile stress due to forces F, acting at the edges along the length of the bar Consider a plane making an angle theta with the length. What are the tensile and shering stresses on this plane ? (a) For what angle is the tensile stress a maximum ? (b) For what angle is the shearing stress a maximum ?

Tensile stress is possible in

A rod area of cross section A is being acted upon by two forces F - F as shown in figure. Consider a section ab of rod whose normal makes angle theta with horimontal. The shear stress upon this section is maximum when theta=(180^(@))/(n) . Find n.

The ratio of tensile stress to the longitudinal strain is defined as

A steel bar of cross-sectional area A and length l is magnetised to develop an intensity of magnetisation l . The pole strength of the bar is