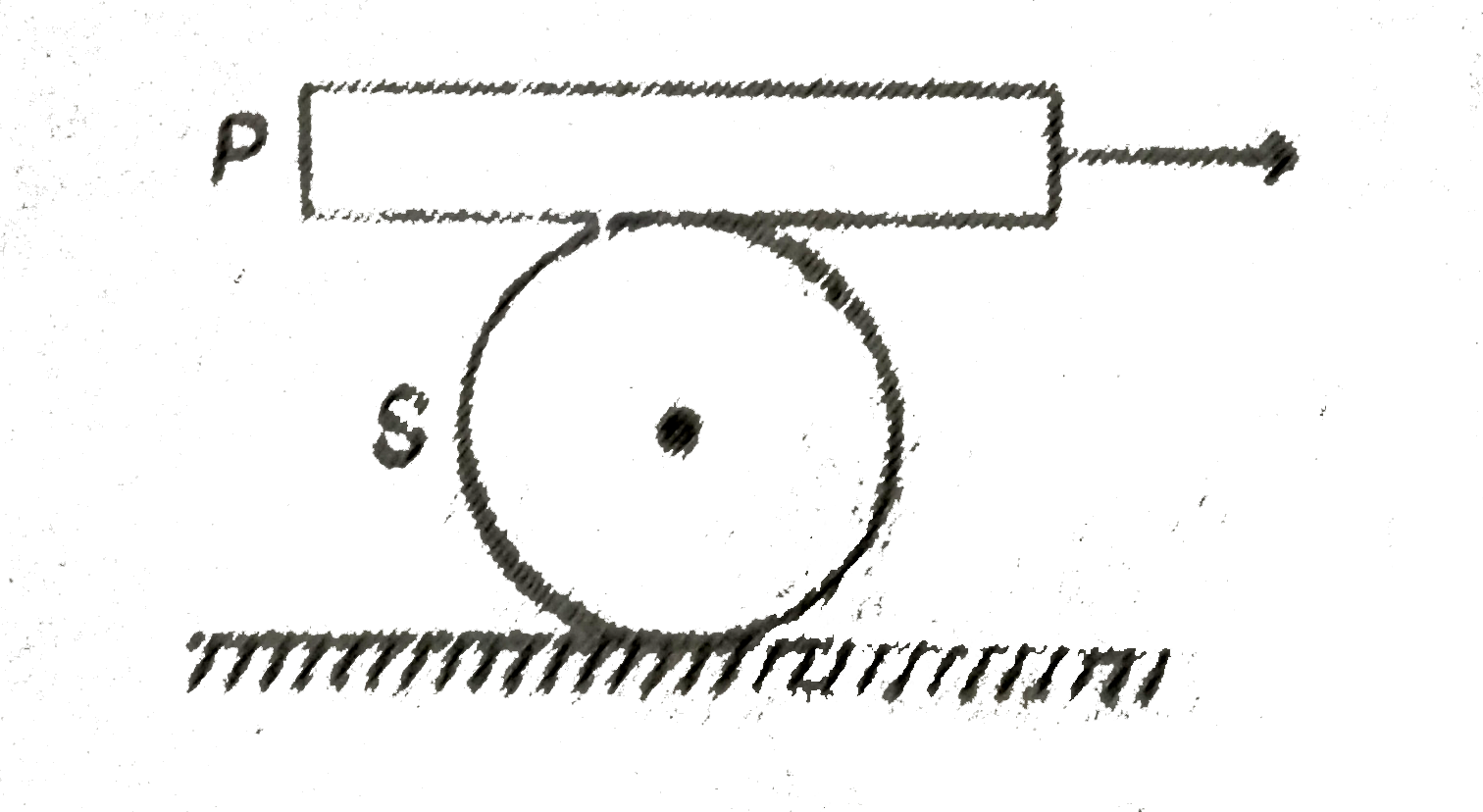A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
ROTATIONAL MOTION
VMC MODULES ENGLISH|Exercise LEVEL - 1 (Mixed Numerical Questions)|15 VideosROTATIONAL MOTION
VMC MODULES ENGLISH|Exercise LEVEL - 2 (Rotatinal Kinematics, Moment of Inertia)|10 VideosROTATIONAL MOTION
VMC MODULES ENGLISH|Exercise LEVEL - 1 (Angular Momentum, Collision)|15 VideosREVISION TEST-2 JEE
VMC MODULES ENGLISH|Exercise PHYSICS|25 VideosSIMPLE HARMONIC MOTION
VMC MODULES ENGLISH|Exercise 7-previous year question|46 Videos
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-ROTATIONAL MOTION -LEVEL - 1 (Mixed topics)
- A uniform cube of side and mass m rests on a rough horizontal surface....
Text Solution
|
- An equilateral prism of mass m rests on a rough horizontal surface wit...
Text Solution
|
- Two rings of same radius and mass are placed such that their centres a...
Text Solution
|
- A plank P is placed on a solid cylinder S, which rolls on a horizontal...
Text Solution
|
- A thin hoop of weight 500 N and radius 1 m rests on a rough inclined p...
Text Solution
|
- A disc is rotated about its axis with a certain angular velocity and l...
Text Solution
|
- An inverted T-shaped object is placed on a horizontal floor as shown i...
Text Solution
|
- A particle of mass 'm' is rigidly attached at 'A' to a ring of mass 3m...
Text Solution
|
- In Fig. the velocities are in ground frame and the cylinder is perform...
Text Solution
|
- A sphere cannot roll without applying force on
Text Solution
|
- When a rigid sphere is projected horizontally with an initial linear v...
Text Solution
|
- A stick of length L and mass M lies on a frictionless horizontal surfa...
Text Solution
|
- In the figure shown, a ring A is initially rolling without sliding wit...
Text Solution
|
- A clockwise torque of 6N-m is applied to the circular cylinder as show...
Text Solution
|
- In both the figures, all other factors are same, except that in figure...
Text Solution
|