Text Solution
Verified by Experts
Topper's Solved these Questions
ROTATIONAL MOTION
VMC MODULES ENGLISH|Exercise JEE Advanced (Archive) (True/False Type)|3 VideosROTATIONAL MOTION
VMC MODULES ENGLISH|Exercise JEE Advanced (Archive) (NUMERICAL VALUE TYPE)|15 VideosREVISION TEST-2 JEE
VMC MODULES ENGLISH|Exercise PHYSICS|25 VideosSIMPLE HARMONIC MOTION
VMC MODULES ENGLISH|Exercise 7-previous year question|46 Videos
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-ROTATIONAL MOTION -JEE Advanced (Archive) (FILL IN THE BLANKS TYPE)
- A particle is projected at time t = 0 from a point P on the ground wit...
Text Solution
|
- A homogeneous rod AB of length L = 1.8 m and mass M is pivoted at the ...
Text Solution
|
- A stone of mass m, tied to the end of a string, is whirled around in a...
Text Solution
|
- A uniform disc of mass m and radius R is rolling up a rough inclined p...
Text Solution
|
- A symmetric lamina of mass M consists of a square shape with a semicir...
Text Solution
|
- Two identical ladders, each of mass M and length L are resting on the ...
Text Solution
|
- A uniform disc of mass m and radius r is projected horizontally with v...
Text Solution
|
- A wedge of mass m and triangular cross- section (AB = BC = CA = 2R) is...
Text Solution
|
- A smooth uniform rod of length L and mass M has two identical beads (1...
Text Solution
|
- A cylinder of mass M and radius R is resting on a horizontal platform ...
Text Solution
|
- A uniform circular disc has radius R and mass m. A particle, also of m...
Text Solution
|
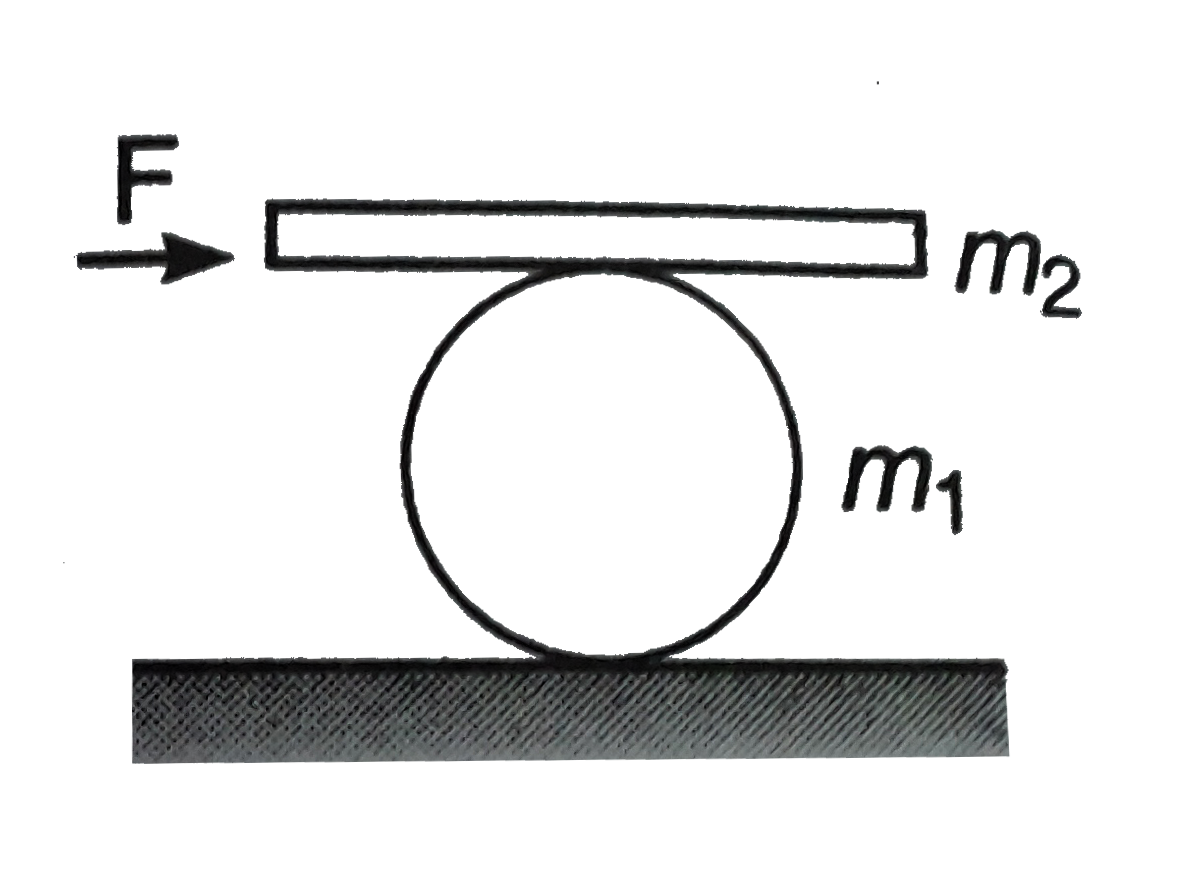
- A man pushes a cylinder of mass m(1) with the help of a plank of mass ...
Text Solution
|
- A rod AB of mass M and length L is lying on a horizontal frictionless ...
Text Solution
|
- Three particles A, B and C each of mass m, are connected to each other...
Text Solution
|