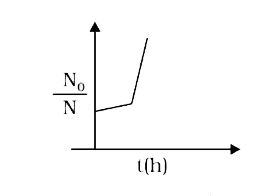
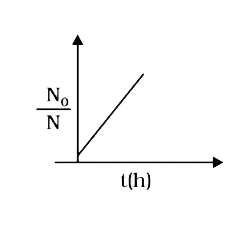
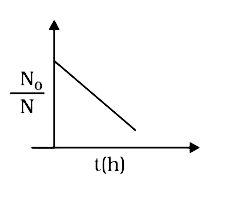
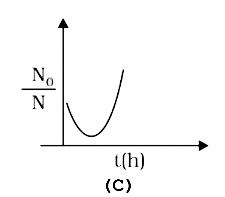
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
CHEMICAL KINETICS
VMC MODULES ENGLISH|Exercise JEE Advanced (Archive)|52 VideosCHEMICAL KINETICS
VMC MODULES ENGLISH|Exercise Level-2 ( Numerical Value Type for JEE Main )|15 VideosCHEMICAL EQUILIBRIUM
VMC MODULES ENGLISH|Exercise IN-CHAPTER EXERCISE - G|10 VideosCHEMICAL THERMODYNAMICS
VMC MODULES ENGLISH|Exercise IN - CHAPTER EXERCISE - L|10 Videos
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-CHEMICAL KINETICS -JEE Main (Archive)
- For the chemical reaction X Y , the standard reaction Gibbs energ...
Text Solution
|
- If a reation follows the Arrhensis equation the plot lnk vs1/(RT) give...
Text Solution
|
- Decomposition of X exhibits a rate constant of 0.5 mu g // year. How ...
Text Solution
|
- For a reaction, consider the plot of In K versus 1//T given in the fig...
Text Solution
|
- Consider the given plots for a reaction obeying Arrhenius equation (0^...
Text Solution
|
- The reactin 2X to B is a zeroth order reaction. If the initial concent...
Text Solution
|
- A bacterial infection in an internal wound grows as N'(t) = N(0) exp (...
Text Solution
|
- The given plots represent the variation of the concentration of a reac...
Text Solution
|
- For the reaction 2A + B rarrC, the values of ini concentrations are gi...
Text Solution
|
- In the following reaction, xA rarryB log(10)[-(d[A])/(dt)]=log(10)[...
Text Solution
|
- NO(2) required for a reaction is produced by the decomposition of N(2)...
Text Solution
|
- For the reaction of H(2) with I(2), the constant is 2.5 xx 10^(-4) dm^...
Text Solution
|
- Consider the given plot of enthalpy of the following reaction between ...
Text Solution
|
- For a reaction scheme Aoverset(k(1))toBoverset(k(2))toD , If the rate ...
Text Solution
|
- For the reaction 2H(2)(g)+2NO(g) rarr N(2)(g)+2H(2)O(g) the observ...
Text Solution
|
- Consider the following plots of rate constant versus (1)/(T) for four ...
Text Solution
|
- For following reactions A overset( 400K)( rarr) Product A underse...
Text Solution
|
- The rate of a certain biochemical reaction at physiological temperatur...
Text Solution
|
- During nuclear explosion, one of the products is""^(90(Sr)) with half-...
Text Solution
|
- Lacto bacillus has generation time 60 min. at 300 K and 40 min. at 400...
Text Solution
|