Home
Class 12
PHYSICS
A man running on a horizontal road at 8 ...

A man running on a horizontal road at 8 km/h finds the rain falling vertically. He increases his speed to 12 km/h and finds that the drops make angle `30^0` with the vertical. Find the speed and direction o the rain with respect to the road.

Text Solution

Verified by Experts

Let the speed of rain with respect to the road is v and the angle formed by rain with vertical is 0.

For the first case
8 = v sin 0.......(i)
For the second case
`12 = v sin 0 +u sin 30^(@)........(ii)`
and `u cos 30^(@) =v cos 0........(iii)`
From (i) and (ii)
`12=8 + u sin 30^(@) rarr u =8 km//h.....(iv)`
From (iii) and (iv) `v cos 0 =sqrt(3)`
`? v^(2)=8^(2) +(4 sqrt(3))^(2) rarr v=4 sqrt(7) km//h`
Promotional Banner

Topper's Solved these Questions

  • Motion in Straight Line

    VMC MODULES ENGLISH|Exercise SOLVED EXAMPLES|20 Videos

  • Motion in Straight Line

    VMC MODULES ENGLISH|Exercise PRACTICE EXERCISE|80 Videos

  • MOTION IN A STRAIGHT LINE & PLANE

    VMC MODULES ENGLISH|Exercise IMPECCABLE|52 Videos

  • Motion in Two Dimensions

    VMC MODULES ENGLISH|Exercise MCQ|2 Videos

Similar Questions

Explore conceptually related problems

A man running on the horizontal road at 8 km h^(-1) find the rain appears to be falling vertically. He incresases his speed to 12 km h^(-1) and find that the drops make angle 30^2 with the vertical. Find the speed and direction of the rain with respedt to the road.

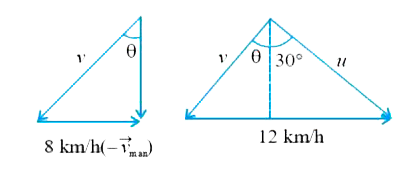
A person walking ,on a horizontal road at 2 km/h finds that the rain is falling vertically . Now the person increasses his speed to 4 km/h and find that rain makes an angle 45^(@) with the vertical . Find the velocity of rain with respect to the road.

A man walking with a speed of 3 km/h finds the rain drops falling vertically downwards. When the man increases his speed to 6km/h he find that the rain drops are falling making an angle of 30^(@) with the vertical . Find the speed of the rain drops ( in km/h)

A man running at a speed of 5 km/h finds that the rain is falling vertically. When the stops running, the finds that the rain is falling at an angle of 60^(@) with the horizontal. The velocity of rain with respect to running man is

To a man walking at the rate of 3 km//h the rain appear to fall vertically downwards. When he increases his speed 6 km//h it appears to meet him at an angle of 45^@ with vertically. Find the speed of rain.

A man starts running along a straight road with uniform velocity observes that the rain is falling vertically downward. If he doubles his speed, he finds that the rain is coming at an angle theta to the vertical. The velocity of rain with respect to the ground is :

A man starts running along a straight road with uniform velocity observes that the rain is falling vertically downward. If he doubles his speed, he finds that the rain is coming at an angle theta to the vertical. The velocity of rain with respect to the ground is :

A man moving with 5 ms^-1 observes rain falling vertically at the rate of 10 m s^-1 . Find the speed and direction of the rain with respect to ground.

To a man walking at the rate of 4 km/h the rain appears to fall vertically. When he increases his speed 8 km/h it appears to meet him at an angle of 45 with vertical. Find the angle made by the velocity of rain with the vertical and its value.

A man when standstill observes the rain falling vertically and when he walks at 4 km//h he has to hold his umberella at an angle 53^(@) from the vertical. Find velocity of the raindrops.